
2.注意30°、60°角的函数值的区别
1.特殊角30°45°60°的四种三角函数值,
计算①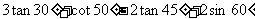 (
( 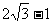 )
)
②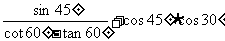 ( 0 )
( 0 )
③ (
(  )
)
④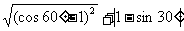 ( 1
)
( 1
)
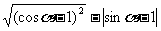 (
(  )
)
注意: ①
②0<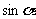 <1, 0<
<1, 0< <1
<1
3.计算:
例3.①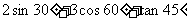 (
(  )
)
② (
(  )
)
③ ( 1 )
( 1 )
④ (
( 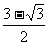 )
)
2.已知特殊角的三角函值求锐角
例2.①已知sinA= ,则∠A= 30° ;
,则∠A= 30° ;
②已知tanA=1,则∠A= 45° ;
③已知cosB= ,则∠B= 60° ;
,则∠B= 60° ;
④已知sinB= ,则∠B= 60° ;
,则∠B= 60° ;
⑤已知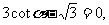 则∠
则∠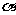 = 60° ;
= 60° ;
⑥已知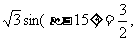 则∠
则∠ 75° ;
75° ;
⑦已知 ,A,B为△ABC的内角,则∠C =
75° ;
,A,B为△ABC的内角,则∠C =
75° ;
⑧已知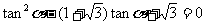 ,则
,则 45°或60° ;
45°或60° ;
1.推导特殊角的三角函数值
例1、直角△ABC中,∠A=30°,求sinA、cosA 、tanA、 cotA
由sin30°= 得出:
得出:
在直角三角形中如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
练习:∠A=45°、∠A=60°呢?
归纳特殊角的三角函数值:
 |
sin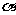 |
cos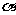 |
tan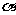 |
cot |
|
30° |
 |
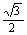 |
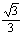 |
 |
|
45° |
 |
 |
1 |
1 |
|
60° |
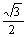 |
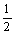 |
 |
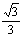 |
2.如图,∠C=90°,AC=7,BC=2
(1) 求∠A和∠B的四个三角函数值
(∠A: ∠B:
∠B: )
)
(2) 比较求值结果,你发现了什么?
(sinA=cosB, cosA=sinB, tanA=cotB, cotA=tanB)
得出:如果两个锐角互余,则有
sin(90°-A)=cosA, cos(90°-A)=sinA,
tan(90°-A)=cotA, cot(90°-A)=tan A
1.什么叫锐角A的正弦、余弦、正切、余切?
P.73 习题25.1 1、2、3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com