
师生共同讨论得出:本题中共有四个随机事件,要分别数出每个随机事件中 的值.学生讨论后归纳出正确数出
的值.学生讨论后归纳出正确数出 的方法:
的方法:
方法1:通过画出的树形图按由上至下,由左至右的方法把每一个可能的结果写出来,从中找出 的值.
的值.
方法2:直接看树形图的最后一步,就可以求出 的值;再由最后一步向上逐个找出符合要求的可能结果,就可以求出
的值;再由最后一步向上逐个找出符合要求的可能结果,就可以求出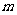 的值了.
的值了.
教师板书:
由树形图可以得到,所有可能出现的结果有12个,这些结果出现的可能性相等.
(1)只有一个元音字母的结果有5个,所以 ;
;
有两个元音字母的结果有4个,所以 ;
;
全部为元音字母的结果有1个,所以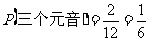 ;
;
(2)全是辅音字母的结果有2个,所以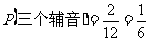 .
.
教师板书:
解:根据题意,我们可以画出如下“树形图”:
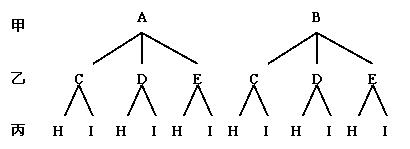
一次试验中有三个步骤,但抽取顺序是不确定的.不妨设抽取顺序为从甲盒取一张、从乙盒取一张、从丙盒取一张.
1、教材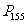 综合运用
综合运用 拓广探索
拓广探索
教学反思
|
25.2 用列举法求概率(第二课时) 郁昌云 教学目标: 1. 理解“包含两步,并且每一步的结果为有限多个情形”的意义。 2. 会用列表的方法求出:包含两步,并且每一步的结果为有限多个情形,这样的试验出现的所有可能结果。 3. 体验数学方法的多样性灵活性,提高解题能力。 教学重点:正确理解和区分一次试验中包含两步的试验。 教学难点:当可能出现的结果很多时,简洁地用列表法求出所有可能结果。 一、比较,区别 出示两个问题: 1.一个布袋中有两个白球和两个黄球,质地和大小无区别,每次摸出1个球,共有几种可能的结果? 2.一个布袋中有两个白球和两个黄球,质地和大小无区别,每次摸出2个球,这样共有几种可能的结果? 要求学生讨论上述两个问题的区别,区别在于这两个问题的每次试验(摸球)中的元素不一样。 二、问题解决 1.例1 教科书第150页例4。 要求学生思考掷两枚硬币产生的所有可能结果。 学生可能会认为结果只有:两个都为正面,一个正面一个反面和两个都是反面这样3种情形,要讲清这种想法的错误原因。 列出了所有可能结果后,问题容易解决。或采用列表的方法,如:
|
正 |
反 |
|
|
正 |
正正 |
正反 |
|
|
反 |
反正 |
反反 |
|
让学生初步感悟列表法的优越性。 2. 问题:“同时掷两枚硬币”,与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗? 同时掷两枚硬币与先后两次掷一枚硬币有时候是有区别的。比如在先后投掷的时候,就会有这样的问题:先出现正面后出现反面的概率是多少?这与先后顺序有关。同时投掷两枚硬币时就不会出现这样的问题。 3.课内练习:书本P151的练习。 三、小结 1.本节课的例题,每次试验有什么特点? 2.用列表法求出所有可能的结果时,要注意表格的设计,做到使各种可能结果既不重复也不遗漏。 四、布置作业: |
本节课应用列举法求概率。
教材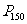 练习
练习 ,
, ,
,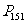 练习
练习
2.一次试验中,各种结果发生的可能性相等.
对于具有上述特点的试验,我们可以从事件所包含的各种可能的结果在全部可能
的试验结果中所占的比分析出事件的概率.
因此,一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相
等,事件A包含其中的、种结果,那么李件A发生的概率为P(A)= 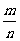
例1.小李手里有红桃1,2,3,4,5,6,从中任抽取一张牌,观察其牌上的数字.求下
列事件的概率.
(1)牌上的数字为3;
(2)牌上的数字为奇数;
(3)牌上的数字为大于3且小于6.
分析:因为从6张牌子任抽取一张符合刚才总结的试验的两个特点,所以可用P(A)= 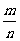 来求解.
来求解.
解:任抽取一张牌子,其出现数字可能为1,2,3,4,5,6,共6种,这些数字出现的可
能性相同.
(1)P(点数为3)=1/6;
(2)P(点数为奇数)=3/6=1/2;
(3)牌上的数字为大于3且小于6的有4,5两种.
所以 P(点数大于3且小于6)=1/3
例2:如图25-7所示,有一个转盘,转盘分成4个相同的扇形,颇色分为红、绿、黄三种颇色,指针的位置固定,转动转盘后任其自由停止.其中的某个扇形会恰好停在指
针所指的位里(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率
(1)指针指向绿色;
(2)指针指向红色或黄色
(3)指针不指向红色.

 分析:转一次转盘,它的可能结果有4种-有限个,并且各种结果发生的可能性相等.因此,它可以应用“ P(A)=
分析:转一次转盘,它的可能结果有4种-有限个,并且各种结果发生的可能性相等.因此,它可以应用“ P(A)= 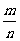 ”问题,即“列举法”求概率.
”问题,即“列举法”求概率.
解,(1) P(指针,向绿色)=1/4;
(2) P(指针指向红色或黄色)=3/4;
(3)P(指针不指向红色)=1/2
例3如图25-8所示是计算机中“扫雷“游戏的画面,在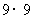 个小方格的正方形雷区中,随机埋藏着
个小方格的正方形雷区中,随机埋藏着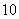 颗地雷,每个小方格内最多只能藏
颗地雷,每个小方格内最多只能藏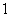 颗地雷。
颗地雷。
小王在游戏开始时随机地踩中一个方格,踩中后出现了如图所示的情况,我们把与标号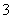 的方格相邻的方格记为
的方格相邻的方格记为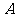 区域(画线部分),
区域(画线部分),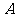 区域外的部分记为
区域外的部分记为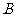 区域,数字
区域,数字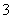 表示在
表示在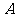 区域中有
区域中有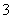 颗地雷,那么第二步应该踩
颗地雷,那么第二步应该踩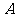 区域还是
区域还是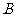 区域?
区域?
分析:第二步应该踩在遇到地雷小的概率,所以现在关键求出在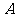 区域、
区域、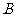 区域的概率并比较。
区域的概率并比较。
解:(1)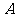 区域的方格共有
区域的方格共有 个,标号
个,标号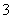 表示在这
表示在这 个方格中有
个方格中有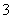 个方格各藏
个方格各藏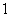 颗地雷,因此,踩
颗地雷,因此,踩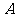 区域的任一方格,遇到地雷的概率是
区域的任一方格,遇到地雷的概率是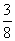 。
。
(2)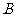 区域中共有
区域中共有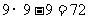 个小方格,其中有
个小方格,其中有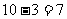 个方格内各藏
个方格内各藏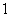 颗地雷。因此,踩
颗地雷。因此,踩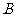 区域的任一方格,遇到地雷的概率是
区域的任一方格,遇到地雷的概率是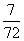 。
。
由于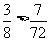 ,所以踩
,所以踩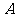 区域遇到地雷的可能性大于踩
区域遇到地雷的可能性大于踩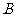 区域遇到地雷的可能性,因而第二步应踩
区域遇到地雷的可能性,因而第二步应踩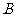 区域。
区域。
1.一次试验中,可能出现的结果有限多个.
2.有1,2,3,4,5,6等6种可能.由于股子的构造相同质地均匀,又是随机掷出的,
所以我们可以断言:每个结果的可能性相等,都是1/6,所以所求概率是1/6所求。
以上两个试验有两个共同的特点:
2.掷一个骰子,向上的一面的点数有多少种可能?向上一面的点数是1的概率是多少?
老师点评:1.可能结果有1,2,3,4,5等5种杯由于纸签的形状、大小相同,又是随机
抽取的,所以我们可以认为:每个号被抽到的可能性相等,都是1/5.其概率是1/5。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com