4、设疑求新法：设立“选择哪个装置呢？” 、 “游戏规则公平吗？”等疑问，要求学生设计游戏规则和提出合理建议，激励学生用创新的思维参与活动。

在教学活动中，我充分利用多媒体辅助教学，直观生动地呈现图片和游戏过程，加强课堂的趣味性以及生动性。同时及时、完整地展示了解题过程，既加大课堂信息量，又提高了教学效率。

另外，我非常重视运用神态、手势和语言对学生进行即兴评价，让他们在充分自信的状态下完成学习过程。

5评价分析

(1)以问题为载体，让学生在不断解决问题的活动中学习，充分体现了学生的主体地位。

(2)以发展思维过程为主线，把传授知识和发展思维有机结合起来，采用引导训练，随堂训练、拓展训练，把问题逐步引向更高的深度和广度，让不同层次的学生得到不同程度的训练，很好地发挥了老师的主导作用。

(3)以培养学生的思维能力为目标，重视概念的提取过程，知识的形成、解题思路的探索过程，使学生在这些过程中展开思维，获取新知识和新方法，提高解决问题的能力，并激发他们的创新意识，认真贯彻了国家课程标准所提出的先进教学理念和教育思想。

以上是我对本节课的初浅认识，希望得到各位专家、各位老师的指导，谢谢大家！

3、以用促学法：从引例、例题、练习、思考题到课题研究，无一不体现在实际生活中用数学。这样就促进了学生参与活动。

2、自主探究法：从发现问题、探究方法、解决问题到归纳总结，很多环节都是教师引导、鼓励学生大胆地自主活动；

1、情境激智法：创设各种情境，激发兴趣，吸引学生积极地参与活动；

3.5布置作业，巩固提高

考虑到学生的个体差异，为促使每一个学生得到不同的发展，同时促进学生对自己的学习进行反思，在第五个环节“布置作业，巩固提高”里作如下安排：

(1)必做题：书本P154/ 3，P155/ 4，5

(2)选做题：

①请设计一个游戏，并用列举法计算游戏者获胜的概率。

②研究性课题：通过调查学校周围道路的交通状况，为交通部门提出合理的建议等。

[设计意图] 通过教学实践作业和社会实践活动，引导学生灵活运用所学知识，让学生把动脑、动口、动手三者结合起来，启发学生的创造性思维，培养协作精神和科学的态度。

4教法分析

根据新教材的特点和学生的实际情况，在本节课我主要采用“引导-发现教学法”。在“问题情境-建立模型-解释、应用与拓展”的基本过程中特别注重通过各种教学手段，激励、启发、引导学生在探索和研究中获取知识、提高能力。例如：

3.4归纳总结，形成能力

我将引导学生从知识、方法、情感三方面来谈一谈这节课的收获。要求每个学生在组内交流，派小组代表发言。

[设计意图] 通过这个环节，可以提高学生概括能力、表达能力，有助于学生全面地了解自己的学习过程，感受自己的成长与进步，增强自信，也为教师全面了解学生的学习状况、因材施教提供了重要依据。

3.3应用新知，深化拓展

为了检验学生对列表法和画树形图法的掌握情况，提高应用所学知识解决问题的能力，在此我选择了教材P154课后练习作为随堂练习。

(1)经过某十字路口的汽车，它可能继续前行，也可能向左或向右，如果这三种可能性大小相同。三辆汽车经过这个十字路口，求下列事件的概率：

①三辆车全部继续前行；

②两辆车向右转，一辆车向左转；

③至少有两辆车向左转。

[随堂练习(1)是一道与实际生活相关的交通问题，可用树形图法来解决。]

(2)在6张卡片上分别写有1--6的整数，随机地抽取一张后放回，再随机地抽取一张，那么第二次取出的数字能够整除第一次取出的数字的概率是多少？

通过解答随堂练习(2)，学生会发现列出的表格和例1的表格完全一样。不同的是：变换了实际背景，设置的问题也不一样。这时，我提出：我们是否可以根据这个表格再编一道用列举法求概率的题目来呢？

为了进一步拓展思维，我向学生提出了这样一个问题，供学生课后思考：

在前面的引例中，转盘的游戏规则是不公平的，你能把它改成一个公平的游戏吗？

[设计意图] 以上问题的提出和解决有利于学生发现数学问题的本质，做到举一反三，融会贯通。

3.2自主分析，再探新知

通过引例的分析，学生对列表法和树形图法求概率有了初步的了解，为了帮助学生熟练掌握这两种方法，我选用了下列两道例题(本节教材P151-P152的例5和例6)。

例1：同时掷两个质地均匀的骰子，计算下列事件的概率：

(1) 两个骰子的点数相同；

(2) 两个骰子的点数的和是9；

(3) 至少有一个骰子的点数为2。

例1是教材上一道“掷骰子”的问题，有了引例作基础，学生不难发现：引例涉及两个转盘，这里涉及两个骰子，实质都是涉及两个因素。于是，学生通过类比列出下列表。

第2个 第1个	1	2	3	4	5	6
1	(1，1)	(1，2)	(1，3)	(1，4)	(1，5)	(1，6)
2	(2，1)	(2，2)	(2，3)	(2，4)	(2，5)	(2，6)
3	(3，1)	(3，2)	(3，3)	(3，4)	(3，5)	(3，6)
4	(4，1)	(4，2)	(4，3)	(4，4)	(4，5)	(4，6)
5	(5，1)	(5，2)	(5，3)	(5，4)	(5，5)	(5，6)
6	(6，1)	(6，2)	(6，3)	(6，4)	(6，5)	(6，6)

　由上表可以看出，同时掷两个骰子，可能出现的结果有36个，它们出现的可能性相等。由所列表格可以发现：

(1)满足两个骰子的点数相同(记为事件A)的结果有6个，即(1，1)，(2，2)，(3，3)，(4，4)，(5，5)，(6，6)，所以P(A)==。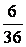

[满足条件的结果在表格的对角线上]

(2)满足两个骰子的点数的和是9(记为事件B)的结果有4个，即(3，6)，(4，5)，(5，4)，(6，3)，所以P(B)==。

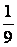[满足条件的结果在(3，6)和(6，3)所在的斜线上]

(3)至少有一个骰子的点数为2(记为事件C)的结果有11个，所以P(C)=。

[满足条件的结果在数字2所在行和2所在的列上]

接着，引导学生进行题后小结：

当一个事件要涉及两个因素并且可能出现的结果数目较多时，通常采用列表法。运用列表法求概率的步骤如下：

①列表 ；

②通过表格计数，确定公式P(A)=中m和n的值；

③利用公式P(A)=计算事件的概率。

分析到这里，我会问学生：“例1题目中的“掷两个骰子”改为“掷三个骰子”，还可以使用列表法来做吗？”由此引出下一个例题。

例2： 甲口袋中装有2个相同的球，它们分别写有字母A和B；乙口袋中3个相同的球，它们分别写有字母C、D和E；丙口袋中2个相同的球，它们分别写有字母H和I。从三个口袋中各随机地取出1个球。

(1)取出的三个球上恰好有1个、2个和3个元音字母的概率分别为多少？

(2)取出的三个球上全是辅音字母的概率是多少？

例2与前面两题比较，有所不同：要从三个袋子里摸球，即涉及到3个因素。此时同学们会发现用列表法就不太方便，可以尝试树形图法。

本游戏可分三步进行。分步画图和分类排列相关的结论是解题的关键。

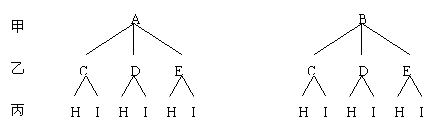
从图形上可以看出所有可能出现的结果共有12个，即：

(幻灯片上用颜色区分)

这些结果出现的可能性相等。

(1)只有一个元音字母的结果(黄色)有5个，即ACH，ADH，BCI，BDI，BEH，所以；

有两个元音的结果(白色)有4个，即ACI，ADI，AEH，BEI，所以；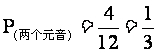

全部为元音字母的结果(绿色)只有1个，即AEI ，所以。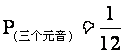

(2)全是辅音字母的结果(红色)共有2个，即BCH，BDH，所以。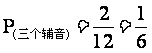

通过例2的解答，很容易得出题后小结：

当一次试验要涉及3个或更多的因素时，通常采用“画树形图”。运用树形图法

求概率的步骤如下：(幻灯片)

①画树形图 ；

②列出结果，确定公式P(A)=中m和n的值；

③利用公式P(A)=计算事件概率。

接着我向学生提问：到现在为止，我们所学过的用列举法求概率分为哪几种情况？ 列表法和画树形图法求概率有什么优越性？什么时候使用“列表法”方便，什么时候使用“树形图法”更好呢？

[设计意图] 通过对上述问题的思考，可以加深学生对新方法的理解，更好的认识到列表法和画树形图法求概率的优越性在于能够直观、快捷、准确地获取所需信息，有利于学生根据实际情况选择正确的方法。

3.1创设情景，发现新知

教材是通过P151-P152的例5、例6来介绍列表法和树形图法的。

例5(教材P151)：同时掷两个质地均匀的骰子，计算下列事件的概率：

(1) 两个骰子的点数相同；

(2) 两个骰子的点数的和是9；

(3) 至少有一个骰子的点数为2。

这个例题难度较大，事件可能出现的结果有36种。若首先就拿这个例题给学生讲解，大多数学生理解起来会比较困难。所以在这里，我将新课的引入方式改为了一个有实际背景的转盘游戏(前一课已有例2作基础)。

(1)创设情景

引例：为活跃联欢晚会的气氛，组织者设计了以下转盘游戏：A、B两个带指针的转盘分别被分成三个面积相等的扇形，转盘A上的数字分别是1，6，8，转盘B上的数字分别是4，5，7(两个转盘除表面数字不同外，其他完全相同)。每次选择2名同学分别拨动A、B两个转盘上的指针，使之产生旋转，指针停止后所指数字较大的一方为获胜者，负者则表演一个节目(若箭头恰好停留在分界线上，则重转一次)。作为游戏者，你会选择哪个装置呢？并请说明理由。

[设计意图] 选用这个引例，是基于以下考虑：以贴近学生生活的联欢晚会为背景，创设转盘游戏引入，能在最短时间内激发学生的兴趣，引起学生高度的注意力，进入情境。

(2)学生分组讨论，探索交流

在这个环节里，首先要求学生分组讨论，探索交流。然后引导学生将实际问题转化为数学问题，即：

“停止转动后，哪个转盘指针所指数字较大的可能性更大呢？”

由于事件的随机性，我们必须考虑事件发生概率的大小。此时我首先引导学生观看转盘动画，同学们会发现这个游戏涉及A、B两转盘， 即涉及2个因素，与前一课所讲授单转盘概率问题(教材P148例2)相比，可能产生的结果数目增多了，列举时很容易造成重复或遗漏。怎样避免这个问题呢？

实际上，可以将这个游戏分两步进行。 于是，指导学生构造表格

(3)指导学生构造表格

首先考虑转动A盘：指针可能指向1，6，8三个数字中的任意一个，可能出现的结果就会有3个。接着考虑转动B盘：当A盘指针指向1时，B盘指针可能指向4、5、7三个数字中的任意一个，这是列举法的简单情况。当A盘指针指向6或8时，B盘指针同样可能指向4、5、7三个数字中的任意一个。一共会产生9种不同的结果。

[设计意图]　这样既分散了难点，又激发了学生兴趣，渗透了转化的数学思想。

(4)学生独立填写表格，通过观察与计算，得出结论(即列表法)

从表中可以发现：A盘数字大于B盘数字的结果共有5种。

∴P(A数较大)=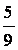 ,　 P(B数较大)=.

　　 ∴P(A数较大)＞ P(B数较大)　

∴选择A装置的获胜可能性较大。

在学生填写表格过程中，注意向学生强调数对的有序性。

由于游戏是分两步进行的，我们也可用其他的方法来列举。即先转动A盘，可能出现1，6，8三种结果；第二步考虑转动B盘，可能出现4，5，7三种结果。

(5)解法二：

由图知：可能的结果为：　 (1，4)，(1，5)，(1，7)，

　　　　　　　(6，4)，(6，5)，(6，7)，

　　　　　　　(8，4)，(8，5)，(8，7)。共计9种。

∴P(A数较大)=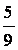 ,　 P(B数较大)=.

　　 ∴P(A数较大)＞ P(B数较大)　

∴选择A装置的获胜可能性较大。

然后，引导学生对所画图形进行观察：若将图形倒置，你会联想到什么？这个图形很像一棵树，所以称为树形图(在幻灯片上放映)。列表和树形图是列举法求概率的两种常用的方法。

[设计意图]自然地学生感染了分类计数和分步计数思想。

3、情感与态度目标 　通过丰富的数学活动，交流成功的经验，体验数学活动充满着探索和创造，体会数学的应用价值，培养积极思维的学习习惯。

3过程分析

《数学课程标准》明确指出：“数学教学是数学活动的教学，学生是数学学习的主人。”为了向学生提供更多从事数学活动的机会，我将本节课的教学过程设定为以下五个环节：