
2.一次试验中,各种结果发生的可能性相等.
对于具有上述特点的试验,我们可以从事件所包含的各种可能的结果在全部可能
的试验结果中所占的比分析出事件的概率.
因此,一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相
等,事件A包含其中的、种结果,那么李件A发生的概率为P(A)= 
例1.小李手里有红桃1,2,3,4,5,6,从中任抽取一张牌,观察其牌上的数字.求下
列事件的概率.
(1)牌上的数字为3;
(2)牌上的数字为奇数;
(3)牌上的数字为大于3且小于6.
分析:因为从6张牌子任抽取一张符合刚才总结的试验的两个特点,所以可用P(A)=  来求解.
来求解.
解:任抽取一张牌子,其出现数字可能为1,2,3,4,5,6,共6种,这些数字出现的可
能性相同.
(1)P(点数为3)=1/6;
(2)P(点数为奇数)=3/6=1/2;
(3)牌上的数字为大于3且小于6的有4,5两种.
所以 P(点数大于3且小于6)=1/3
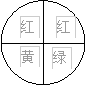
例2:如图25-7所示,有一个转盘,转盘分成4个相同的扇形,颇色分为红、绿、黄三种颇色,指针的位置固定,转动转盘后任其自由停止.其中的某个扇形会恰好停在指
针所指的位里(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率
(1)指针指向绿色;
(2)指针指向红色或黄色
(3)指针不指向红色.
 分析:转一次转盘,它的可能结果有4种-有限个,并且各种结果发生的可能性相等.因此,它可以应用“ P(A)=
分析:转一次转盘,它的可能结果有4种-有限个,并且各种结果发生的可能性相等.因此,它可以应用“ P(A)=  ”问题,即“列举法”求概率.
”问题,即“列举法”求概率.
解,(1) P(指针,向绿色)=1/4;
(2) P(指针指向红色或黄色)=3/4;
(3)P(指针不指向红色)=1/2
例3如图25-8所示是计算机中“扫雷“游戏的画面,在 个小方格的正方形雷区中,随机埋藏着
个小方格的正方形雷区中,随机埋藏着 颗地雷,每个小方格内最多只能藏
颗地雷,每个小方格内最多只能藏 颗地雷。
颗地雷。
小王在游戏开始时随机地踩中一个方格,踩中后出现了如图所示的情况,我们把与标号 的方格相邻的方格记为
的方格相邻的方格记为 区域(画线部分),
区域(画线部分), 区域外的部分记为
区域外的部分记为 区域,数字
区域,数字 表示在
表示在 区域中有
区域中有 颗地雷,那么第二步应该踩
颗地雷,那么第二步应该踩 区域还是
区域还是 区域?
区域?
分析:第二步应该踩在遇到地雷小的概率,所以现在关键求出在 区域、
区域、 区域的概率并比较。
区域的概率并比较。
解:(1) 区域的方格共有
区域的方格共有 个,标号
个,标号 表示在这
表示在这 个方格中有
个方格中有 个方格各藏
个方格各藏 颗地雷,因此,踩
颗地雷,因此,踩 区域的任一方格,遇到地雷的概率是
区域的任一方格,遇到地雷的概率是 。
。
(2) 区域中共有
区域中共有 个小方格,其中有
个小方格,其中有 个方格内各藏
个方格内各藏 颗地雷。因此,踩
颗地雷。因此,踩 区域的任一方格,遇到地雷的概率是
区域的任一方格,遇到地雷的概率是 。
。
由于 ,所以踩
,所以踩 区域遇到地雷的可能性大于踩
区域遇到地雷的可能性大于踩 区域遇到地雷的可能性,因而第二步应踩
区域遇到地雷的可能性,因而第二步应踩 区域。
区域。
1.一次试验中,可能出现的结果有限多个.
2.有1,2,3,4,5,6等6种可能.由于股子的构造相同质地均匀,又是随机掷出的,
所以我们可以断言:每个结果的可能性相等,都是1/6,所以所求概率是1/6所求。
以上两个试验有两个共同的特点:
2.掷一个骰子,向上的一面的点数有多少种可能?向上一面的点数是1的概率是多少?
老师点评:1.可能结果有1,2,3,4,5等5种杯由于纸签的形状、大小相同,又是随机
抽取的,所以我们可以认为:每个号被抽到的可能性相等,都是1/5.其概率是1/5。
不管求什么事件的概率,我们都可以做大量的试脸.求频率得概率,这是上一节课也是刚才复习的内容,它具有普遍性,但求起来确实很麻烦,是否有比较简单的方法,这
种方法就是我们今天要介绍的方法-列举法,
把学生分为10组,按要求做试验并回答问题.
1.从分别标有1,2,3 ,4,5号的5根纸签中随机地抽取一根.抽出的号码有多少种?其抽到1的概率为多少?
教科书第155页习题25.2第9题。
这是一道正确理解概率意义的问题,在学生深入思考的基础上教师要着重分析解题的思路
2. 为了正确地求出所求的概率,我们要求出各种可能的结果,那么通常是用什么方法求出各种可能的结果呢?
特点:一次试验中可能出现的结果是有限多个,各种结果发生的可能性是相等的。
通常可用列表法求得各种可能结果,具体有直接分析列出可能结果,列表法和树形图法。
问题:(要求学生思考和讨论)
1. 本单元学习的概率问题有什么特点?
教科书第154页练习。
练习1是每次试验涉及2个因素的问题,共有36种可能的结果;
练习2是每次试验涉及3个因素的问题,共有27种可能的结果。
尽管这2个问题可能的结果都比较多,但用树形图的方法并不难求得,重要的是要让学生正确把握题意,鉴别每次试验涉及的因素以及这些因素的顺序。
例1 同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点子数相同;(2)两个骰子的点子数的和是9;(3)至少有一个骰子的点数为2。
分析:由于每个骰子有6种可能结果,所以2个骰子出现的可能结果就会有很多,我们用怎样的方法才能既不重复又不遗漏地求出所有可能的结果呢?这个问题要让学生充分发表意见,在次基础上再使学生认识到列表法可以清楚地列出所有可能的结果,体会其优越性。
列出表格。也可用树形图法。
其实,求出所有可能的结果的方法不止是列表法,还有树形图法也是有效的方法,要让学生体验它们各自的特点,关键是对所有可能结果要做到:既不重复也不遗漏。
板书解答过程。
思考:教科书第152页的思考题。
例2 教科书第152页例6。
分析:弄清题意后,先让学生思考从3个口袋中每次各随机地取出一个球,共3个球,这就是说每一次试验涉及到3个因素,这样的取法共有多少种呢?你打算用什么方法求得? 在学生充分思考和交流的前提下,老师介绍树形图的方法。
第一步可能产生的结果为A和B,两者出现的可能性相同且不分先后,写在第一行。
第二步可能产生的结果有C、D和E,三者出现的可能性相同且不分先后,从A和B分别画出三个分支,在分支下的第二行分别写上C、D和E。
第三步可能产生的结果有两个H和I,两者出现的可能性相同且不分先后,从C、D和E分别画出两个分支,在分支下的第三行分别写上H和I。(如果有更多的步骤可依上继续)
第四步按竖向把各种可能的结果竖着写在下面,就得到了所有可能的结果的总数。再找出符合要求的种数,就可以利用概率和意义计算概率了。
教师要详细地讲解以上各步的操作方法。
写出解答过程。
问:此题可以用列表法求出所有可能吗?
小结:教科书第153页左边的结论。
思考:教科书第153页的思考题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com