11．50,10,0.26；200

9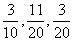． ；　　　　 10. 0.1,0.2,0.4,0.2,0.075,0.025；0.1

1．D　　 2．B　　 3．B　　 4．A　　　　 5．C　　 6．C　　 7．C　　　　 8．B　　

16．理论上讲，两个随机正整数互质的概率为P=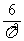．请你和你班上的同学合作，每人随机写出若干对正整数(或自己利用计算器产生)，共得到n对正整数，找出其中互质的对数m，计算两个随机正整数互质的概率，利用上面的等式估算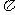的近似值．

解答

13．甲、乙两同学开展“投球进筐”比赛，双方约定：① 比赛分6局进行，每局在指定区域内将球投向筐中，只要投进一次后该局便结束；② 若一次未进可再投第二次，以此类推，但每局最多只能投8次，若8次投球都未进，该局也结束；③ 计分规则如下：a. 得分为正数或0；b. 若8次都未投进，该局得分为0；c. 投球次数越多，得分越低；d.6局比赛的总得分高者获胜 .

(1) 设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进，请你按上述约定，用公式、表格或语言叙述等方式，为甲、乙两位同学制定一个把n换算为得分M的计分方案；

(2) 若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数，“×”表示该局比赛8次投球都未进)：

根据上述计分规则和你制定的计分方案，确定两人谁在这次比赛中获胜.

12．小颖有20张大小相同的卡片，上面写有1~20这20个数字，她把卡片放在一个盒子中搅匀，每次从盒中抽出一张卡片，记录结果如下：

(1)完成上表；

(2)频率随着实验次数的增加，稳定于什么值左右？

(3)从试验数据看，从盒中摸出一张卡片是3的倍数的概率估计是多少？

(4)根据推理计算可知，从盒中摸出一张卡片是3的倍数的概率应该是多少？

11．为配和新课程的实施，某市举行了“应用与创新”知识竞赛，共有1万名学生参加了这次竞赛(满分100分，得分全为整数)。为了解本次竞赛成绩情况，从中随机抽取了部分学生的竞赛成绩，进行统计，整理见下表：

表中a=________,b=________, c＝_______；若成绩在90分以上(含90分)的学生获一等奖，估计全市获一等奖的人数为___________．

10．红星养猪场400头猪的质量(质量均为整数千克)频率分布如下，其中数据不在分点上

从中任选一头猪，质量在65kg以上的概率是_____________．　

9． 同时抛掷两枚硬币，按照正面出现的次数，可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果，小红与小明两人共做了6组实验，每组实验都为同时抛掷两枚硬币10次，下表为实验记录的统计表：

由上表结果，计算得出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是___________________．当试验组数增加到很大时，请你对这三种结果的可能性的大小作出预测：______________．

8．某学生调查了同班同学身上的零用钱数，将每位同学的零用钱数记录了下来(单位：元)：2，5，0，5，2，5，6，5，0，5，5，5，2，5，8，0，5，5，2，5，5，8，6，5，2，5，5，2，5，6，5，5，0，6，5，6，5，2，5，0.

假如老师随机问一个同学的零用钱，老师最有可能得到的回答是(　 )．

A． 2元　　 B．5元　　　 C．6元　　　 D．0元