什么叫仰角、俯角？

P82 　习题25.3　　2、3

2.　　　 学会几何建模，通过解Rt△求解.

1.　　　 了解仰角、俯角的概念.

例3.如图，为了测量顶部不能达到的建筑物AB的高度，现在地平面上取一点C，用测量仪测得A点的仰角为45°，再向前进20米取一点D，使点D在BC延长线上，此时测得A的仰角为30°，已知测量仪的高为1.5米，求建筑物AB的高度.

解：在Rt△AEG中，EG==AG，在Rt△AFG中，

FG==AG∴EF=FE－EG=(－1)AG=20，

∴AG=+11.5(米)

答：建筑物AB的高度为(+11.5)米.

说明：解此类问题的关键是建立实际问题的数学模型，即构建Rt△.必要时可添加适当的辅助线，解题时应选择适当的关系式进行解题，并按照题目中的要求进行近似计算.

变式：若点E在FG的延长线上，且∠AEG=45°，已知FE的长度，其他条件不变，如何求建筑物AB的高度？　　　

例4.如图，在一座山的山顶处用高为1米的测顶器望地面C、D两点，测得俯角分别为

60°和45°，若已知DC长为20㎝，求山高.

分析：已知∠FAD=45°，∠FAC=60°，要求山高，只需求AE.

解；设AE=，在Rt△ADE中，，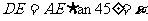

在R△ACE中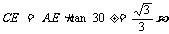，，DC=DE－CE=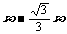=20，

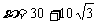∴，∴BE=AE－AB=29+10，

∴山高为(29+10)米.

例1．书P80　 例3

例2.如图，线段AB、CD分别表示甲、乙两幢楼，AB⊥CD，CD⊥BD，从甲楼顶A测乙楼顶C的仰角=30°，已知甲楼高15米，两楼水平距离为24米，求乙楼高.

解：Rt△ACE中，CE==8m，∴CD=CE+DE=CE+AB=(8+15)(米)

答：乙楼高为(8+15)米.

2.一棵树AC在地面上的影子BC为10米，在树影一端B测得树顶A的俯角为

　　　 45°，则树高　　 米；若仰角为60°，树高　　 米.(精确到1米)

5.俯角：视线在水平线的下方，视线与水平线的夹角.

练习：1.由A测得B的仰角为36°，由B去测A时的俯角为　　 .

铅垂线　　　 几个概念　 1.铅垂线

2.水平线

　　 仰角　　　　　 3.视线

　　 俯角　　　　　 4.仰角：视线在水平线的上方，视线与水平线的夹角.

P82 　习题25.3　　1