
P82 习题25.3 4
2、 在复杂图形中求解时要结合图形,理解题意,运用所学知识通过构造直角三角形求解。
1、 理解坡度、坡角的概念
P82 练习1
 例4.沿水库拦水坝的背水坡,将坝顶加宽2m,坡度由原来的1:2改为1:2.5,已知坝高6m,坝长50m,求:
例4.沿水库拦水坝的背水坡,将坝顶加宽2m,坡度由原来的1:2改为1:2.5,已知坝高6m,坝长50m,求:
① 加宽部分横断面的面积
② 完成这一工程需要的土方是多少?
分析:加宽部分的横断面AFEB为梯形,故通过
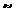
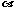
作梯形的高构造直角三角形,利用坡度的变化求解。
解:①设梯形ABCD为原大坝的横截面图,梯形AFEB为加宽部分,
过A、F分别作AG⊥BC于G,FH⊥BC于H,
在直角△ABG中,由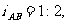 AG=6,得BG=12
AG=6,得BG=12
在直角△EFH中,由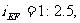 FH=6,得EH=15
FH=6,得EH=15
∴EB=EH-BH=EH-(BG-HG)=15-(12-2)=5
∴SAFEB=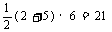 ㎡
㎡
②V=50×SAFEB=21×50=1050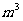
3、 堤坝横断面是等腰梯形,(如图所示)
堤坝横断面是等腰梯形,(如图所示)
① 若AB=10,CD=4,高h=4,则坡度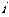 =
=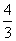 ,AD= 5
,AD= 5
②若AB=10,CD=4 ,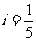 ,则
,则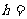 2 ,
2 , 
例1、书P81 例4
例2、如图,水库堤坝的横断面成梯形ABCD,DC∥AB,迎水坡AD长为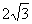 米,上底DC长为2米,背水坡BC长也为2米,又测得∠DAB=30°,∠CBA=60°,求下底AB的长.
米,上底DC长为2米,背水坡BC长也为2米,又测得∠DAB=30°,∠CBA=60°,求下底AB的长.
 解:过D、C分别作DE⊥AB于E,CF⊥AB于F,
解:过D、C分别作DE⊥AB于E,CF⊥AB于F,
在直角△ADE中,∠A=30°,AD=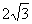
∴DE=AD sin30°=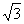 ,AE=AD cos30°=3. 30°
60°
,AE=AD cos30°=3. 30°
60°
在直角△CBF中,BF=BC cos60°=1
∴AB=AE+EF+BF=3+2+1=6
答:下底的长为6米。
思考:延长两腰或平移一腰能求出下底的长吗?
说明:以上解法体现了“转化”思想,把梯形的有关问题转化为解直角三角形可多角度的分析,添加辅助线,灵活、恰当地构造直角三角形,使解法合理化。
例3.铁道路基的横断面是等腰梯形,其尺寸如图所示,其中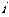 =1:1.5是坡度每修1m长的这种路基,需要土石多少立方?
=1:1.5是坡度每修1m长的这种路基,需要土石多少立方?
解:过A、D分别作AE⊥BC于E,DF⊥BC于F.则AE=DF=1.2m.
 ∵
∵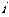 =1:1.5.ABCD为等腰梯形.
=1:1.5.ABCD为等腰梯形.
∴BE=CF=1.8m
∴BC=1.8+10+1.8=13.6m
∴SABCD=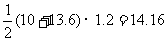 ㎡
㎡
∴V=1×14.16=14.16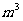
答:需要土面14.16立方米。
2、若一斜坡的坡面的余弦为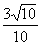 ,则坡度
,则坡度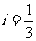 ,
,
4、坡角 :坡面与水平面的夹角
:坡面与水平面的夹角 .
. 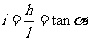
显然,坡度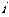 越大,坡角
越大,坡角 就越大,坡面就越陡。
就越大,坡面就越陡。
练习:1、沿山坡前进10米,相应升高5米,则山坡坡度 ,坡角 30°,
,坡角 30°,
3、坡度(坡比)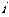 :坡面的铅垂高度
:坡面的铅垂高度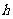 和水平长度
和水平长度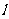 的比
的比

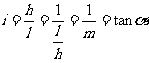
 几个概念:
1、铅垂高度
几个概念:
1、铅垂高度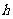
2、水平长度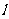
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com