2、学情分析：通过前面的学习，学生已有两个基础：一是已经初步了解利用频率估计概率的方法；二是学生对研究键盘上字母的排列规律是感兴趣的.

1、地位与作用：初中这次课程改革，把概率统计内容引进来，这是因为：在生活实际中，许多问题的解决，都涉及到概率统计的内容.新课标要求学生学会两种求概率的方法：古典概型，用列表法或数形图；当试验的所有可能不是有限个，或发生的可能性不相等时，用频率来估计概率.本节课作为课题学习课，它被安排在初中概率统计部分的最后，具有很高的综合性和活动性.课程标准要求掌握利用频率估计概率的方法.

　 P86， 11，12，13

运用所学知识解决实际问题，学会几何建模，通过解Rt△求解

　 P85， 6，7，8

例4.　　　　　 如图，A城气象部门测得今年第9号台风上午8时在A城南偏东30°的海面生成，并以每小时40海里的速度向正北方向移动，上午10时测得台风中心移到了A城南偏东45°的方向，若台风中心120海里的范围内将受台风影响，问A城是否会受9号台风影响？

分析：A城是否会受台风影响，就是A城到台风移动路线BC的距离是否大于120千米。

解：过A作AE⊥BC于E，设AE=EC=，则BE=，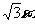

∵BC=2×40=80，∴BC=BE-CE=(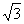-1)=80，

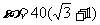∴≈109.2＜120，

∴A城会受台风影响。

例1.　　　　　 如图△ABC中，∠B=45°，∠C=60，AD⊥BC于D，AD=2，

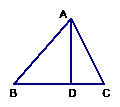求：(1)BC的长　　 (2)S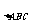

解：(1)∵AD⊥BC，∠B=45°，∠C=60°，AD=2

　　　　　　　　　 ∴BD=2，CD=　　 ∴BC=2+

　　　　　　　 (2)∴S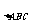=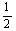×2×(2+)=2+

例2.　　　　　 如图，为调整数学格局，充分发挥资源优势，现将地处A、B两地的两所技校合并成职业技术教育中心，为方便A、B两校师生的交往，学校准备在相距5千米的A、B两地修筑一条笔直公路AB，经测量，在A地的北偏东60°方向，B地的西偏北45°方向的C处有一半径为1.8千米的湖泊，问计划修筑的这条公路会不会穿过湖泊？

分析：要想知道公路会不会穿过湖泊，就必须知道点C到AB的距离是否大于1.8千米。

解：过C作CD⊥AB于D

由题意知∠CAD=30°，在Rt△ACD中，AD=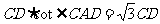，在Rt△BCD中，同理可得CD=DB，∴AB=AD+BD=(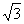+1)CD=5，∴CD≈1.84(千米)＞1.8千米

答：计划修筑的这条公路不会穿过湖泊。

例3.　　　　　 如图，河对岸有一电线杆CD，从A点测得电线杆顶端的仰角为18°，前进30米，到B处测得D点的仰角为36°，求电线杆的高度(精确到0.1米)

解：∵∠ADB=∠DBC-∠A=36°-18°=18°=∠A，∴DB=AB=30，

在Rt△ABC中，CD=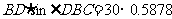≈17.6(米)

答：电线杆的高度约为17.6米。

3.Rt△ABC中，∠C=90°，斜边上中线CD=3，AC=3.6，tan∠DCB=

2.Rt△ABC中，∠A=90°,sinB=,c=2,则b=

1.Rt△ABC中，∠C=90°,CD⊥AB于D,若AD=2，CD=4,则tanB=