
4、顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为___________________.
3、、二次函数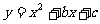 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )(A)
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )(A)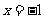 (B)
(B)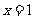 (C)
(C)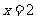 (D)
(D)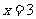
2、已知抛物线y=x2+(n-3)x+n+1经过坐标原点O,求这条抛物线的顶点P的坐标
1、抛物线y=(k+1)x2+k2-9开口向下,且经过原点,则k=---------
26.1 二次函数章节练习
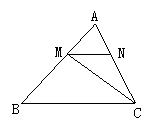
3.如图所示,△ABC中,BC=4,∠B=45°,AB=3 ,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.
,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.
(1)求出S与x之间的函数关系式,并写出自变量x的取值范围.
(2)是否存在平行于BC的线段MN,使△MNC的面积等于2?若存在,请求出MN的长; 若不存在,请说明理由.
2.已知:如图所示,BD为⊙O的直径,且BD=8,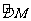 是圆周的
是圆周的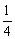 ,A为
,A为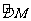 上任意一点, 取AC=AB,交BD的延长线于C,连结OA,并作AE⊥BD于E,设AB=x,CD=y.
上任意一点, 取AC=AB,交BD的延长线于C,连结OA,并作AE⊥BD于E,设AB=x,CD=y.
(1)写出y关于x的函数关系式;
(2)当x为何值时,CA是⊙O的切线?
(3)当CA与⊙O相切时,求tan∠OAE的值.
1.某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元, 在销售过程中发现,当销售单价定为100元时,年销售时为20万件;销售单价每增加10元, 年销售量将减少1万件.设第一年销售单价为x元,销售量为y万件,获利(年获利=年销售额-生产成本-投资)为z万元.
(1)试写出y与x之间的函数关系式;(不必写出x的取值范围)
(2)试写出z与x之间的函数关系式;(不必写出x的取值范围)
(3)计算销售单价为160元时的获利,并说明同样的获利,销售单价还可以定为多少元?相应的销售量分别为多少万件?
12.(2004,黄冈,11分)心理学家研究发现,一般情况下, 学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强, 中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力y随时间t的变化规律有如下关系式:
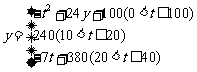
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较, 何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
11.(2002,昆明,8分)某广告公司设计一幅周长为12米的矩形广告牌, 广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围.
(2)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少?(精确到元)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com