
2.抛物线y=ax2+bx+c(a≠0)的图象:当a>0时,开口向上,当a<0时开口向下,对称轴是直线x= ,顶点坐标是(
,顶点坐标是( ).
).
1.二次函数y=ax2,y=a(x-h)2,y=a(x-h)2+k,y=ax2+bx+c(各式中,a≠0)的图象形状相同,只是位置不同,它们的顶点坐标及对称轴如下表:
|
解析式 |
y=ax2 |
y=a(x-h)2 |
y=a(x-h)2+k |
y=ax2+bx+c |
|
顶点坐标 |
(0,0) |
(h,0) |
(h,k) |
(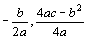 ) ) |
|
对 称 轴 |
x=0 |
x=h |
x=h |
x=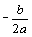 |
当h>0时,y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到, 当h<0时,则向左平行移动|h|个单位得到. 当h>0,k>0时,将抛物线y=ax2向右平行移动h个单位,再向上移动k个单位,就可以得到y=a(x-h)2+k的图象; 当h>0,k<0时,将抛物线y=ax2向右平行移动h个单位,再向下移动|k|个单位可得到y=a(x-h)2+k的图象; 当h<0,k>0时,将抛物线向左平行移动|h|个单位,再向上移动k个单位可得到y=a(x-h)2+k的图象; 当h<0,k<0时,将抛物线向左平行移动|h|个单位,再向下移动|k|个单位可得到y=a(x-h)2+k的图象; 因此,研究抛物线 y=ax2+bx+c(a≠0)的图象,通过配方,将一般式化为y=a(x-h)2+k的形式,可确定其顶点坐标、对称轴,抛物线的大体位置就很清楚了.这给画图象提供了方便.
3.会根据已知图象上三个点的坐标求出二次函数的解析式.
名师精讲
2.能利用图象或配方法确定抛物线的开口方向及对称轴、顶点的位置.
1.会用描点法画出二次函数的图象.
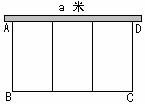
8、 富根老伯想利用一边长为a米的旧墙及可以围成24米长的旧木料,建造猪舍三间,如图,它们的平面图是一排大小相等的长方形。
(1) 如果设猪舍的宽AB为x米,则猪舍的总面积S(米2)与x有怎样的函数关系?
(2) 请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC和宽AB的长度?旧墙的长度是否会对猪舍的长度有影响?怎样影响?
7、一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s(米)与时间t(秒)的数据如下表:
|
时间t(秒) |
1 |
2 |
3 |
4 |
… |
|
距离s(米) |
2 |
8 |
18 |
32 |
… |
写出用t表示s的函数关系式。
6、若 是二次函数,求m的值。
是二次函数,求m的值。
5、函数y=ax2+bx+c (a、b、c是常数),问当a、b、c满足什么条件时,
(1)它是二次函数?
(2)它是一次函数?
(3)它是正比例函数?
4、已知一个直角三角形的两条直角边的和为10cm。
(1)求这个直角三角形的面积S与其中一条直角边长x之间的函数关系式和自变量x的取值范围;
(2)求当x=5cm时直角三角形的面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com