函数y＝x²、y=-x²、y=2x²、y=-2x²是函数y=ax²的特例，由函数y＝x²、y=-x²、y＝2x²、y=-2x²的图象的共同特点，可猜想：

　　 函数y=ax²的图象是一条________，它关于______对称，它的顶点坐标是______。

　　 如果要更细致地研究函数y=ax²图象的特点和性质，应如何分类？为什么?

　　 让学生观察y＝x²、y＝2x²的图象，填空；

　　 当a>0时，抛物线y=ax²开口______，在对称轴的左边，曲线自左向右______；在对称轴的右边，曲线自左向右______，______是抛物线上位置最低的点。

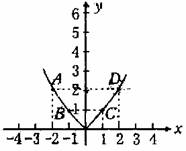　　 图象的这些特点反映了函数的什么性质?

先让学生观察下图，回答以下问题；

　　 (1)X_A、X_B大小关系如何?是否都小于0？

　　 (2)y_A、y_B大小关系如何?

　　 (3)X_C、X_D大小关系如何?是否都大于0?

　　 (4)y_C、y_D大小关系如何?

　　 (X_A<X_B，且X_A<0，X_B<0；y_A>y_B；X_C<X_D，且X_C>0，X_D>0，y_C<y_D)

　　 其次，让学生填空。

　　 当X<0时，函数值y随着x的增大而______，当X>O时，函数值y随X的增大而______；当X＝______时，函数值y=ax² (a>0)取得最小值，最小值y=______

　　 以上结论就是当a>0时，函数y=ax²的性质。

　　 思考以下问题：

　　 观察函数y＝-x²、y=-2x²的图象，试作出类似的概括，当a<O时，抛物线y＝ax²有些什么特点?它反映了当a<O时，函数y=ax²具有哪些性质?

　　 让学生讨论、交流，达成共识，当a<O时，抛物线y=ax²开口向上，在对称轴的左边，曲线自左向右上升；在对称轴的右边，曲线自左向右下降，顶点抛物线上位置最高的点。图象的这些特点，反映了当a<O时，函数y=ax²的性质；当x<0时，函数值y随x的增大而增大；与x>O时，函数值y随x的增大而减小，当x=0时，函数值y＝ax²取得最大值，最大值是y＝0。

3．将所画的四个函数的图象作比较，你又能发现什么?

　 对于1，在学生画函数图象的同时，教师要指导中下水平的学生，讲评时，要引导学生讨论选几个点比较合适以及如何选点。两个函数图象的共同点以及它们的区别，可分组讨论。交流，让学生发表不同的意见，达成共识，两个函数的图象都是抛物线，都关于y轴对称，顶点坐标都是(0，0)，区别在于函数y=x²的图象开口向上，函数y=-x²的图象开口向下。

　　 对于2，教师要继续巡视，指导学生画函数图象，两个函数的图象的特点；教师可引导学生类比1得出。

　　 对于3，教师可引导学生从1的共同点和2的发现中得到结论：四个函数的图象都是抛物线，都关于y轴对称，它的顶点坐标都是(0，0)．

2．在同一直角坐标系中，画出函数y=2x²与y=-2x²的图象，观察并比较这两个函数的图象，你能发现什么?

1．在同一直角坐标系中，画出函数y=x²与y=-x²的图象，观察并比较两个图象，你发现有什么共同点？又有什么区别?

　例1、画二次函数y=ax²的图象。

解：(1)列表：在x的取值范围内列出函数对应值表：

　(2)在直角坐标系中描点：用表里各组对应值作为点的坐标，在平面直角坐标系中描点

　(3)连线：用光滑的曲线顺次连结各点，得到函数y=x²的图象，如图所示。

提问：观察这个函数的图象，它有什么特点?

让学生观察，思考、讨论、交流，归结为：它有一条对称轴，且对称轴和图象有一点交点。

抛物线概念：像这样的曲线通常叫做抛物线。

顶点概念：抛物线与它的对称轴的交点叫做抛物线的顶点．

3．一次函数的图象是什么？二次函数的图象是什么?

　　 1，同学们可以回想一下，一次函数的性质是如何研究的?

　　 (先画出一次函数的图象，然后观察、分析、归纳得到一次函数的性质)

2．我们能否类比研究一次函数性质方法来研究二次函数的性质呢?如果可以，应先研究什么?

　　 (可以用研究一次函数性质的方法来研究二次函数的性质，应先研究二次函数的图象)

1．请叙述二次函数的定义．

　　 2，许多实际问题可以转化为二次函数来解决，请你联系生活实际，编一道二次函数应用题，并写出函数关系式。

2．P3练习第1，2题。

1.(口答)下列函数中，哪些是二次函数?

　　 (1)y=5x+1　　 (2)y=4x²－1

　　 (3)y=2x³－3x²　　 (4)y=5x⁴－3x+1