
2.难点:理解二次例函数的概念.
1.重点:理解二次例函数的概念,能根据已知条件写出函数解析式
3.情感态度与价值观:
通过对几个特殊的二次函数的讲解,向学生进行一般与特殊的辩证唯物主义教育
2.过程与方法目标;
通过“探究----感悟----练习”,采用探究、讨论等方法进行。
1.知识与技能目标:
⑴.使学生理解并掌握二次例函数的概念
⑵.能判断一个给定的函数是否为二次例函数,并会用待定系数法求函数解析式
⑶.能根据实际问题中的条件确定二次例函数的解析式,体会函数的模型思想
课本作业题
本节课你有什么收获?
例1、已知二次函数 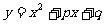 当x=1时,函数值是4;当x=2时,函数值是-5。求这个二次函数的解析式。
当x=1时,函数值是4;当x=2时,函数值是-5。求这个二次函数的解析式。
此题难度较小,但却反映了求二次函数解析式的一般方法,可让学生一边说,教师一边板书示范,强调书写格式和思考方法。
练习:已知二次函数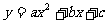 ,当x=2时,函数值是3;当x=-2时,函数值是2。求这个二次函数的解析式。
,当x=2时,函数值是3;当x=-2时,函数值是2。求这个二次函数的解析式。
例2、如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形(图中阴影部分)。设AE=BF=CG=DH=x(cm) ,四边形EFGH的面积为y(cm2),求:
(1) y关于x 的函数解析式和自变量x的取值范围。
(2) 当x分别为0.25,0.5,1.5,1.75时,对应的四边形EFGH的面积,并列表表示。

方法:
(1)学生独立分析思考,尝试写出y关于x的函数解析式,教师巡回辅导,适时点拨。
(2)对于第一个问题可以用多种方法解答,比如:
求差法:四边形EFGH的面积=正方形ABCD的面积-直角三角形AEH的面积DE4倍。
直接法:先证明四边形EFGH是正方形,再由勾股定理求出EH2
(3)对于自变量的取值范围,要求学生要根据实际问题中自变量的实际意义来确定。
(4)对于第(2)小题,在求解并列表表示后,重点让学生看清x与y 之间数值的对应关系和内在的规律性:随着x的取值的增大,y的值先减后增;y的值具有对称性。
练习:
用20米的篱笆围一个矩形的花圃(如图),设连墙的一边为x,矩形的面积为y,求:
(1)写出y关于x的函数关系式 .
.
(2)当x=3时,矩形的面积为多少? 
(二) 做一做
1、 下列函数中,哪些是二次函数?
(1)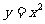 (2)
(2) 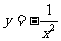 (3)
(3) 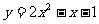 (4)
(4)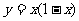
(5)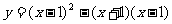
2、分别说出下列二次函数的二次项系数、一次项系数和常数项:
(1)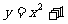 (2)
(2) (3)
(3)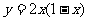
3、若函数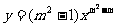 为二次函数,则m的值为 。
为二次函数,则m的值为 。
(二)上述三个函数解析式具有哪些共同特征?
让学生充分发表意见,提出各自看法。
教师归纳总结:上述三个函数解析式经化简后都具y=ax²+bx+c (a,b,c是常数, a≠0)的形式.
板书:我们把形如y=ax²+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数(quadratic function)
称a为二次项系数, b为一次项系数,c为常数项,
请讲出上述三个函数解析式中的二次项系数、一次项系数和常数项
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com