5．已知抛物线y＝ax²+bx+c与直线y＝x－2相交于(m，－2)，(n，3)两点，且抛物线的对称轴为直线x＝3，求函数的关系式。

4．已知抛物线y₁＝x²+x－k与直线y＝－2x+1的交点的纵坐标为3。

　　 (1)求抛物线的关系式；

　　 (2)求抛物线y＝x²+x－k与直线y＝－2x+1的另一个交点坐标．

3．填空。

　　 (1)抛物线y＝x²－x－2与x轴的交点坐标是______，与y轴的交点坐标是______。

　 　(2)抛物线y＝2x²－5x+3与y轴的交点坐标是______，与x轴的交点坐标是______。

2．利用函数的图象求下列方程的解。(1)、，　　 (2)、

1. 利用函数的图象求下列方程的解：(1)x²+x－6＝0；　　 (2)2x²－3x－5＝0

2．你能根据方程组：的解的情况，来判定函数y＝x²与y＝bx+c图象交点个数吗?请说说你的看法。

　 　已知抛物线y₁＝2x²－8x+k+8和直线y₂＝mx+1相交于点P(3，4m)。

　　 (1)求这两个函数的关系式；

　　 (2)当x取何值时，抛物线与直线相交，并求交点坐标。

　　 解：(1)因为点P(3，4m)在直线y₂＝mx+1上，所以有4m＝3m+1，解得m＝1

　　 所以y₁＝x+1，P(3，4)。　　 因为点P(3，4)在抛物线y₁＝2x²－8x+k+8上，所以有

　　 4＝18－24+k+8　　 解得　 k＝2　　 所以y₁＝2x²－8x+10

　　 (2)依题意，得　　解这个方程组，得，

　　 所以抛物线与直线的两个交点坐标分别是(3，4)，(1.5，2.5)。

　　 利用图26．3．4(见P24页)，运用小刘方法求下列方程的解，并检验小刘的方法是否合理。

　　 (1)x²+x－1＝0(精确到0.1)；　　 (2)2x²－3x－2＝0。

　　 教学要点：①要把(1)的方程转化为x²＝－x+1，画函数y＝x²和y＝－x+1的图象；

　　 ②要把(2)的方程转化为x²＝x+1，画函数y＝x²和y＝x+1的图象；③在学生练习的同时，教师巡视指导；④解的情况分别与复习两道题的结果进行比较。

5．如果函数y＝x²和y＝bx+c图象没有交点，一元二次方程x²＝bx+c的解怎样?

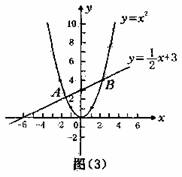　　 问题1：(P23问题4)育才中学初三(3)班学生在上节课的作业中出现了争论：求方程x²＝x十3的解时，几乎所有学生都是将方程化为x²－x－3＝0，画出函数y＝x²－x－3的图象，观察它与x轴的交点，得出方程的解。唯独小刘没有将方程移项，而是分别画出了函数y＝x²和y＝x+2的图象，如图(3)所示，认为它们的交点A、B的横坐标－和2就是原方程的解．

　　 提问：　　 1. 这两种解法的结果一样吗?　　 2．小刘解法的理由是什么?

让学生讨论，交流，发表不同意见，并进行归纳。

3．函数y＝x²和y＝bx+c的图象一定相交于两点吗?你能否举出例子加以说明?

　　 4，函数y＝x²和y＝bx+c的图象的交点横坐标一定是一元二次方程x²＝bx+c的解吗?