
1.知识与能力:
复习巩固用函数y=ax2+bx+c的图象求方程ax2+bx+c=0的解.
26.2 用函数的观点看一元二次方程(2)
教学目标:
2.若二次函数y=ax2+bx+c的图象与x轴无交点,试说明,元二次方程ax2+bx+c=0和一元二次不等式ax2+bx+c>0、ax2+bx+c<0的解的情况.
问题1:某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高为0.8m.水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示.
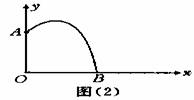
根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+.
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内?
问题2:画出函数y=x2-x-3/4的图象,根据图象回答下列问题.
(1)图象与x轴交点的坐标是什么;
(2)当x取何值时,y=0?这里x的取值与方程x2-x-=0有什么关系?
(3)你能从中得到什么启发?
对于问题(2),教师组织学生分组讨论、交流,各组选派代表发表意见,全班交流,达成共识:从“形”的方面看,函数y=x2-x-的图象与x轴交点的横坐标,即为方程x2-x-=0的解;从“数”的方面看,当二次函数y=x2-x-的函数值为0时,相应的自变量的值即为方程x2-x-=0的解.更一般地,函数y=ax2+bx+c的图象与x轴交点的横坐标即为方程ax2+bx+c=0的解;当二次函数y=ax2+bx+c的函数值为0时,相应的自变量的值即为方程ax2+bx+c=0的解,这一结论反映了二次函数与一元二次方程的关系.
在现实生活中,我们常常会遇到与二次函数及其图象有关的问题,如拱桥跨度、拱高计算等,利用二次函数的有关知识研究和解决这些问题,具有很现实的意义.本节课,请同学们共同研究,尝试解决以下几个问题.
|
用函数观点看一元二次方程 抛物线y=ax2+bx+c与方程ax2+bx+c=0的解之间的关系 例题 |
总结本节的知识点.
例 利用函数图象求方程x2-2x-2=0的实数根(精确到0.1).
解:作y=x2-2x-2的图象(图26.2-3),它与x轴的公共点的横坐标大约是-0.7,2.7.
所以方程x2-2x-2=0的实数根为x1≈-0.7,x2≈2.7.
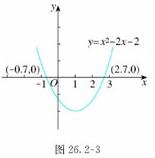
播放课件:函数的图象与求解一元二次方程的解,前一个课件用来画图,可根据图像估计出方程x2-2x-2=0实数根的近似解,后一个课件可以准确的求出方程的解,体会其中的差异.
一般地,从二次函数y=ax2+bx+c的图象可知,
(1)如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数的值是0,因此x=x0就是方程ax2+bx+c=0的一个根.
(2)二次函数的图象与x轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点.这对应着一元二次方程根的三种情况:没有实数根,有两个相等的实数根,有两个不等的实数根.
由上面的结论,我们可以利用二次函数的图象求一元二次方程的根.由于作图或观察可能存在误差,由图象求得的根,一般是近似的.
二次函数(1)y=x2+x-2;
(2) y=x2-6x+9;
(3) y=x2-x+0.
的图象如图26.2-2所示.
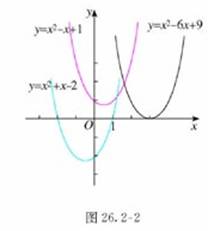
(1)以上二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?
(2)当x取公共点的横坐标时,函数的值是多少?由此,你能得出相应的一元二次方程的根吗?
先画出以上二次函数的图象,由图像学生展开讨论,在老师的引导下回答以上的问题.
可播放课件:函数的图像,输入a,b,c的值,划出对应的函数的图像,观察图像,说出函数对应方程的解.
可以看出:
(1)抛物线y=x2+x-2与x轴有两个公共点,它们的横坐标是-2,1.当x取公共点的横坐标时,函数的值是0.由此得出方程x2+x-2=0的根是-2,1.
(2)抛物线y=x2-6x+9与x轴有一个公共点,这点的横坐标是3.当x=3时,函数的值是0.由此得出方程x2-6x+9=0有两个相等的实数根3.
(3)抛物线y=x2-x+1与x轴没有公共点, 由此可知,方程x2-x+1=0没有实数根.
总结:一般地,如果二次函数y=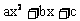 的图像与x轴相交,那么交点的横坐标就是一元二次方程
的图像与x轴相交,那么交点的横坐标就是一元二次方程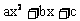 =0的根.
=0的根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com