4.若二次函数y=-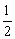x²+bx+c的图象与x轴相交于A(-5,0),B(-1,0).

　 (1)求这个二次函数的关系式;

　 (2)如果要通过适当的平移,使得这个函数的图象与x轴只有一个交点,那么应该怎样平移?向右还是向左?或者是向上还是向下?应该平移向个单位?

3.请画出适当的函数图象,求方程x²=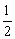x+3的解.

2.已知下表:

　 (1)求a、b、c的值，并在表内空格处填入正确的数；

　 (2)请你根据上面的结果判断:

　　 ①是否存在实数x,使二次三项式ax²+bx+c的值为0?若存在,求出这个实数值;若不存在,请说明理由.

②画出函数y=ax²+bx+c的图象示意图,由图象确定,当x取什么实数时,ax²+ bx+c>0?

1.已知二次函数y=ax²-5x+c的图象如图所示,请根据图象回答下列问题:

　 (1)a=_______,c=______.

　 (2)函数图象的对称轴是_________,顶点坐标P__________.

　 (3)该函数有最______值,当x=______时,y最值=________.

　 (4)当x_____时,y随x的增大而减小.

　　　 当x_____时,y随x的增大而增大.

(5)抛物线与x轴交点坐标A_______,B________;

与y轴交点C 的坐标为_______;

=_________,=________.

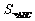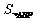　 (6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.

　 (7)方程ax²-5x+c=0中△的符号为________.方程ax²-5x+c=0的两根分别为_____,____.

　 (8)当x=6时,y______0;当x=-2时,y______0.

26.2用函数观点看一元二次方程(2)

●基础探究

已知抛物线y₁＝2x²－8x+k+8和直线y₂＝mx+1相交于点P(3，4m).

　　 (1)求这两个函数的关系式；

　　 (2)当x取何值时，抛物线与直线相交，并求交点坐标.

　　 解：(1)因为点P(3，4m)在直线y₂＝mx+1上，所以有4m＝3m+1，解得m＝1

　　 所以y₁＝x+1，P(3，4).　　 因为点P(3，4)在抛物线y₁＝2x²－8x+k+8上，所以有

　　 4＝18－24+k+8　　 解得　 k＝2　　 所以y₁＝2x²－8x+10

　　 (2)依题意，得　　解这个方程组，得，

　　 所以抛物线与直线的两个交点坐标分别是(3，4)，(1.5，2.5).

2．完成以下两道题：

　　 (1)画出函数y＝x²+x－1的图象，求方程x²+x－1＝0的解.(精确到0.1)

　　 (2)画出函数y＝2x²－3x－2的图象，求方程2x²－3x－2＝0的解.

1．如何运用函数y＝ax²+bx+c的图象求方程ax²+bx+c的解?

3．情感、态度与价值观：

提高学生综合解题能力，渗透数形结合思想.

教学重点；用函数图象法求方程的解以及提高学生综合解题能力是教学的重点.

教学难点：提高学生综合解题能力，渗透数形结合的思想是教学的难点.

教学方法：

学生学法：

教学过程：

2．方法与过程：

让学生体验函数y＝x²和y＝bx+c的交点的横坐标是方程x²＝bx+c的解的探索过程，掌握用函数y＝x²和y＝bx+c图象交点的方法求方程ax²＝bx+c的解.