
1.已知函数y=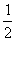 x2-x-12,当函数y随x的增大而减小时,x的取值范围是( )
x2-x-12,当函数y随x的增大而减小时,x的取值范围是( )
A. x<1 B. x>1 C. x>-4 D. -4<x<6
26.3 实际问题与二次函数(1)
4、(1)
y=-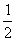 (x-2)(x+3)
(2)m=2 E(-2,2)
(x-2)(x+3)
(2)m=2 E(-2,2)

4.已知抛物线经过A(-3,0)、B(0,3)、C(2,0)三点.
(1) 求这条抛物线的解析式;
(2) 如果点D(1,m)在这条抛物线上,求m值和点D关于这条抛物线对称轴的对称点E的坐标,并求出tan∠ADE的值.
答案:1、C 2、能射中球门 3、(1)y=- (x+2)(x-3)
(2) 5
(x+2)(x-3)
(2) 5
3.已知二次函数的图象与x轴交于A(-2,0)、B(3,0)两点,且函数有最大值是2.
(1) 求二次函数的图象的解析式;
(2) 设次二次函数的顶点为P,求△ABP的面积.
2.在一场足球赛中,一球员从球门正前方10米处将球踢起射向球门,当球飞行的水平距离为6米时,球到达最高点,此时球高3米,已知球门高为2.44米,问能否射中球门?
1.用长为8米的铝合金条做成如图所示形状的矩形窗框,是窗户的透光面积最大,那么这个窗户的最大透光面积是( )
 A.
A. 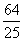 m2
B.
m2
B. 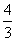 m2
m2
 C.
C.
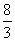 m2
D. 4 m2
m2
D. 4 m2
26.3 实际问题与二次函数(2)
24、已知:如图,一次函数的图象经过第一、二、三象限,且与反比例函数的图象交于A、B两点,与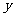 轴交于点C,与
轴交于点C,与 轴交于点D,OB=
轴交于点D,OB=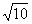 ,tan∠BOD=
,tan∠BOD=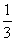 。
。
①求反比例函数的解析式;
②设点A的横坐标为 ,△ABO的面积为
,△ABO的面积为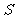 ,求
,求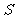 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
③当△OCD的面积等于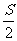 时,试判断过A、B两点的抛物线在
时,试判断过A、B两点的抛物线在 轴上裁得的线段长能否等于3。如果能,求此时抛物线的解析式;如果不能,请说明理由。(12分)
轴上裁得的线段长能否等于3。如果能,求此时抛物线的解析式;如果不能,请说明理由。(12分)

23、为配合客户不同要求,某通讯公司有A、B两种优惠计划,以供客户选择,列表如下:
|
服 务 项 目 |
计划A |
计划B |
|
即时直接对话+自动数字传呼 |
即时直接对话+自动数字传呼 |
|
|
每月基本服务费(座机费) |
50元 |
98元 |
|
免费通话时间 |
首60分钟 |
首300分钟 |
|
以后每分钟收费 |
0.40元 |
0.40元 |
请根据上面提供的信息,解答下列问题:
(1)设通话时间为 (分钟),所需付出的费用为
(分钟),所需付出的费用为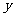 (元)。分别写出计划A、计划B中的
(元)。分别写出计划A、计划B中的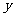 与
与 之间的函数关系式;
之间的函数关系式;
(2)通话时间超过多少分钟时,计划B才会比计划A更优?
(3)若用户决定选择计划B,最多可以比选择A便宜多少费用?(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com