
1. 二次函数的图象的顶点在原点,且过点(2,4),求这个二次函数的关系式。
2.选用课时作业优化设计,
每一课时作业优化设计
1.P19习题 26.2 4.(1)、(3)、5。
例1.如图所示,求二次函数的关系式。
分析:观察图象可知,A点坐标是(8,0),C点坐标为(0,4)。从图中可知对称轴是直线x=3,由于抛物线是关于对称轴的轴对称图形,所以此抛物线在x轴上的另一交点B的坐标是(-2,0),问题转化为已知三点求函数关系式。
解:观察图象可知,A、C两点的坐标分别是(8,0)、(0,4),对称轴是直线x=3。因为对称轴是直线x=3,所以B点坐标为(-2,0)。
设所求二次函数为y=ax2+bx+c,由已知,这个图象经过点(0,4),可以得到c=4,又由于其图象过(8,0)、(-2,0)两点,可以得到解这个方程组,得
所以,所求二次函数的关系式是y=-x2+x+4
练习: 一条抛物线y=ax2+bx+c经过点(0,0)与(12,0),最高点的纵坐标是3,求这条抛物线的解析式。
问题1:能不能以A点为原点,AB所在直线为x轴,过点A的x轴的垂线为y轴,建立直角坐标系?
让学生了解建立直角坐标系的方法不是唯一的,以A点为原点,AB所在的直线为x轴,过点A的x轴的垂线为y轴,建立直角坐标系也是可行的。
问题2,若以A点为原点,AB所在直线为x轴,过点A的x轴的垂直为y轴,建立直角坐标系,你能求出其函数关系式吗?
分析:按此方法建立直角坐标系,则A点坐标为(0,0),B点坐标为(4,0),OC所在直线为抛物线的对称轴,所以有AC=CB,AC=2m,O点坐标为(2;0.8)。即把问题转化为:已知抛物线过(0,0)、(4,0);(2,0.8)三点,求这个二次函数的关系式。
二次函数的一般形式是y=ax2+bx+c,求这个二次函数的关系式,跟以前学过求一次函数的关系式一样,关键是确定o、6、c,已知三点在抛物线上,所以它的坐标必须适合所求的函数关系式;可列出三个方程,解此方程组,求出三个待定系数。
解:设所求的二次函数关系式为y=ax2+bx+c。
因为OC所在直线为抛物线的对称轴,所以有AC=CB,AC=2m,拱高OC=0.8m,
所以O点坐标为(2,0.8),A点坐标为(0,0),B点坐标为(4,0)。
由已知,函数的图象过(0,0),可得c=0,又由于其图象过(2,0.8)、(4,0),可得到解这个方程组,得 所以,所求的二次函数的关系式为y=-x2+x。
问题3:根据这个函数关系式,画出模板的轮廓线,其图象是否与前面所画图象相同?
问题4:比较两种建立直角坐标系的方式,你认为哪种建立直角坐标系方式能使解决问题来得更简便?为什么?
(第一种建立直角坐标系能使解决问题来得更简便,这是因为所设函数关系式待定系数少,所求出的函数关系式简单,相应地作图象也容易)
 请同学们阅渎P18例7。
请同学们阅渎P18例7。
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶。它的拱高AB为4m,拱高CO为0.8m。施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
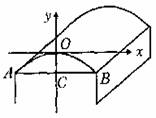 分析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数关系式,然后根据这个关系式进行计算,放样画图。
分析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数关系式,然后根据这个关系式进行计算,放样画图。
如图所示,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系。这时,屋顶的横截面所成抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式为: y=ax2 (a<0) (1)
因为y轴垂直平分AB,并交AB于点C,所以CB= =2(cm),又CO=0.8m,所以点B的坐标为(2,-0.8)。
因为点B在抛物线上,将它的坐标代人(1),得 -0.8=a×22 所以a=-0.2
因此,所求函数关系式是y=-0.2x2。
请同学们根据这个函数关系式,画出模板的轮廓线。
5.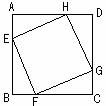 如图,正方形EFGH的顶点在边长为a的正方形ABCD的边上,若AE=x,正方形EFGH的面积为y.
如图,正方形EFGH的顶点在边长为a的正方形ABCD的边上,若AE=x,正方形EFGH的面积为y.
(1) 求出y与x之间的函数关系式;
(2) 正方形EFGH有没有最大面积?若有,试确定E点位置;若没有,说明理由.
答案:1、A 2、售价为35元时,在半月内可获得最大利润 3、(1) (2)
(2)
(3)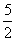 4、①略 ②4倍 5、(1)y=2x2-2ax+a2 (2) 有.当点E是AB的中点时,面积最大.
4、①略 ②4倍 5、(1)y=2x2-2ax+a2 (2) 有.当点E是AB的中点时,面积最大.
4.当运动中的汽车撞到物体时,汽车所受到的损坏程度可以用“撞击影响”来衡量.某型汽车的撞击影响可以用公式I=2v2来表示,其中v(千米/分)表示汽车的速度.
① 列表表示I与v的关系;
② 当汽车的速度扩大为原来的2倍时,撞击影响扩大为原来的多少倍?
3. 某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是
某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是 .请回答下列问题:
.请回答下列问题:
(1) 柱子OA的高度是多少米?
(2) 喷出的水流距水平面的最大高度是多少米?
(3) 若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池外?
2.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,如果提高售价,才能在半月内获得最大利润?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com