1.通过对实际问题情景的分析确定二次函数的表达式，体会二次函数的意义.

3、学到了哪些思考问题的方法？

2、解决问题的一般步骤是什么？应注意哪些问题？

1、这节课学习了用什么知识解决哪类问题？

设问：用长为8m的铝合金条制成如图形状的矩形窗框，

问窗框的宽和高各是多少米时，窗户的透光面积最大？最大面积是多少？

引导学生分析，板书解题过程。

变式(即课本例1)：现在用长为8米的铝合金条制成如图所示的窗框(把矩形的窗框改为上部分是由4个全等扇形组成的半圆，下部分是矩形)，那么如何设计使窗框的透光面

积最大？(结果精确到0.01米)

探究一:某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出20件，已知商品的进价为每件40元，如何定价才能使利润最大？

(1)题目中有几种调整价格的方法？

(2)题目涉及到哪些变量？哪一个量是自变量？哪些量随之发生了变化？

分析: 调整价格包括涨价和降价两种情况

先来看涨价的情况：⑴设每件涨价x元，则每星期售出商品的利润y也随之变化，我们先来确定y与x的函数关系式。涨价x元时则每星期少卖　　　 件，实际卖出　 　　　　　件,销额为　　　　　　　　　　　　　　 元，买进商品需付　　　　　 　元因此，所得利润为　　　　　　　　元

即:y=-10x²+100x+6000　 (0≤X≤30)

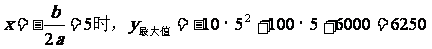
所以，当定价为65元时，利润最大，最大利润为6250元

可以看出，这个函数的图像是一

条抛物线的一部分，这条抛物线

的顶点是函数图像的最高点，也

就是说当x取顶点坐标的横坐标

时，这个函数有最大值。由公式

可以求出顶点的横坐标.

小结:解这类问题一般的步骤:

(1)列出二次函数的解析式，并根据自变量的实际意义，确定自变量的取值范围；

(2)在自变量的取值范围内，运用公式法或通过配方求出二次函数的最大值或最小值。

给你长8m的铝合金条，设问：

①你能用它制成一矩形窗框吗？

②怎样设计，窗框的透光面积最大？

③如何验证？

6．如图是抛物线拱桥，已知水位在AB位置时，水面宽4米，水位上升3米就达到警戒线CD，这时水面宽4米，若洪水到来时，水位以每小时0.25米速度上升，求水过警戒线后几小时淹到拱桥顶?

5．已知二次函数y＝ax²+bx+c的图象过A(0，－5)，B(5，0)两点，它的对称轴为直线x＝2，求这个二次函数的关系式。

4．已知二次函数y＝ax²+bx+c的图象经过A(0，1)，B(－1，0)，C(1，0)，那么此函数的关系式是______。如果y随x的增大而减少，那么自变量x的变化范围是______。