
问题1 要用长20米的铁栏杆,一面靠墙,围成一个矩形的花圃,怎样围法才能使围成的花圃的面积最大?
试一试(1)设矩形花圃的垂直于墙的一边长为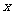 米,先取
米,先取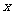 的一些值,算出矩形的另一边的长,进而得出矩形的面积y.
的一些值,算出矩形的另一边的长,进而得出矩形的面积y.
(2)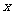 的值是否可以任意取?有限定范围吗?
的值是否可以任意取?有限定范围吗?
(3)发现,当长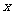 确定后,矩形的面积
确定后,矩形的面积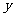 也随之确定,
也随之确定,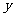 是
是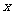 的函数,试写出这个函数关系式.
的函数,试写出这个函数关系式.
问题2 某商店将每件进价为8元的某种商品按每件10元出售,一天可以售出约100件.该店想通过降低售价、增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低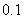 元,其销售量可增加约10件.将这种商品的售价降低多少时,能使销售利润最大?
元,其销售量可增加约10件.将这种商品的售价降低多少时,能使销售利润最大?
4.解:(1)设抛物线的解析式为y= ,由对称轴是y轴得b=0,
,由对称轴是y轴得b=0,
由EO=6,得c=6,又抛物线经过点D(4,2),
所以:16a+6=2,解得a=
所求抛物线的解析式为y=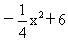 。
。
(2)取x=±2.4,代入(1)所求得的解析式中,求得y=4.56>4.2
故这辆货运卡车能通过隧道.
26. 解:(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1)
设抛物线的解析式是y=a(x-5)2+5
把(0,1)代入y=a(x-5)2+5得a=-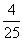
∴y=-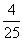 (x-5)2+5(0≤x≤10)
(x-5)2+5(0≤x≤10)
(2)由已知得两景观灯的纵坐标都是4
∴4=-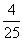 (x-5)2+5 ∴
(x-5)2+5 ∴ 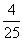 (x-5)2=1 ∴x1=
(x-5)2=1 ∴x1= x2=
x2=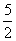
∴ 两景观灯间的距离为5米.
4、 本节课后,你是否探求出更好的解题方法?
3、 本节课后,你还可以联想到什么问题?
2、 本节课中,你有什么不满意之处?
1、 本节课中,你有何疑问?
(二)、实际生活中的推广
4.如图,宜昌西陵长江大桥属于抛物线形悬索桥,桥面(视为水平的)与主悬钢索之间用垂直钢拉索连接.桥两端主塔塔顶的海拔高度均是187.5米,桥的单孔跨度(即两主塔之间的距离)900米,这里水面的海拔高度是74米.
若过主塔塔顶的主悬钢索(视为抛物线)最低点离桥面(视为直线)的高度为0.5米,桥面离水面的高度为19米.请你计算距离桥两端主塔100米处垂直钢拉索的长.(结果精确到0.1米)

5. 右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
右图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
(1)求抛物线的解析式.(6分)
(2)求两盏景观灯之间的水平距离.(4分)
6.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系。y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)如果该隧道内设双行道,现有一辆货运卡车高4.2m,宽2.4米,这辆货运卡车能否通过该隧道?通过计算说明你的结论.

22. 解:(方法一)如图,以桥面上位于主悬钢索最低点的正下方一点坐标原点,以桥面(上竖直钢拉索与桥面连接点,不答此点不扣分)所在的直线为x轴建立平面直角坐标系.…2分,
解:(方法一)如图,以桥面上位于主悬钢索最低点的正下方一点坐标原点,以桥面(上竖直钢拉索与桥面连接点,不答此点不扣分)所在的直线为x轴建立平面直角坐标系.…2分,
则A(0,0.5),B(-450, 94.5),…4分
C(450,94.5).
由题意,设抛物线为:y=ax2+0.5…5分
将C(450,94.5)代入求得:
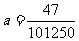 或
或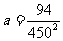 .
.
∴ ……6分
……6分
当x=350时,y=57.4;当x=400时,y=74.8.…7分
∴离桥两端主塔100米处竖直钢拉索的长都约为57.4米,离桥两端主塔50米处竖直钢拉索的长都约为74.8米.
(方法二)如图,以抛物线形主悬钢索最低点为原点,以平行于桥面的[竖直钢拉索与桥面连接点所在的(不答此点不扣分)]直线为x轴建立平面直角坐标系.…2分
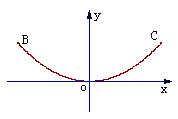 则B(- 450,
94),C(450,94).…3分
则B(- 450,
94),C(450,94).…3分
设抛物线为:y=ax2 .……………4分
将C(450,94)代入求得:
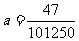 或
或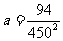 .∴
.∴ .…5分
.…5分
当x =350时, y = 56.9,当x=400时, y=74.3.…6分
∴56.9+0.5=57.4, 74.3+0.5=74.8.…7分
∴离桥两端主塔100米处竖直钢拉索的长约为57.4米,离桥两端主塔50米处竖直钢拉索的长约为74.8米.
(一)、体育课中的推广
1.实验报告.
1.实验目的:研究怎样才能将铅球推得更远?
2.实验器械:铅球、皮尺、测角仪.
3.实验过程:
小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.
4.实验结果和建议.
如下图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
|
推铅球的方向与 水平线的夹角 |
30° |
45° |
60° |
|
铅球运行所得到 的抛物线解析式 |
y1=-0.06(x-3)2+2.5 |
y2=______(x-4)2+3.6 |
y3=-0.22(x-3)2+4 |
|
估测铅球在最 高点的坐标 |
P1( , ) |
P2 (4,3.6) |
P3(3,4) |
|
铅球落点到小明站 立处的水平距离 |
9.5m |
10m |
( )m |
⑴请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
 ⑵请根据以上数据,对如何将铅球推得更远提出你的建议.
⑵请根据以上数据,对如何将铅球推得更远提出你的建议.
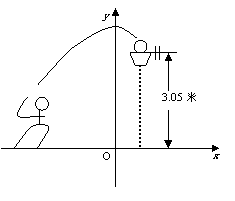
2.如图一位篮球运动员跳起投篮,球沿抛物线 运行,已知篮框的中心离地面的距离为3.05米.
运行,已知篮框的中心离地面的距离为3.05米.
(1)球在空中运行的最大高度为多少?
(2)如果该运动员跳投时,球出手离地面的高度为2.25米,他距离篮框中心的水平距离是4米,请问能否准确落入篮框内?
3.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数 (t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
(A)0.71s (B) 0.70s (C)0.63s (D)0.36s

|
问题情景 |
学生成果展 |
心得体会 |
|
1.看一看,想一想 你知道吗,平时我们在跳绳时,绳甩到最高处的形状是什么? |
|
|
|
2.试一试 正在甩绳的甲、乙两名学生拿绳的手间距(AB)为6米,距地面均为(AC)0.9米,身高(EF)为1.4米的小丽站在距甲的水平距离为1米地方,绳子甩到最高处时刚好通过她的头顶. 你能建立几种不同的直角坐标系. 你认为哪一种直角坐标系的建立,有利于求二次函数的解析式. 对你以后建立直角坐标系有什么启发? |
 |
|
|
3.一般来说二次函数解析式有几种不同的表达方式? |
|
|
|
4.胡老师也建立了直角坐标系,你能很快求出解析式吗? |
|
|
|
|
5.绳子甩到最高处时,最高点离地面有多高? |
与二次函数的什么内容相关. |
|
|
|
6.如果姚明想参加我们的活动,他不弯腰能跳吗? |
|
|
|
|
7.像小丽的身高最适宜在哪一段跳绳?请求出X的范围? |
|
|
|
8.如果小华站在离甲水平距离为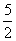 米处跳,且绳子甩到最高处时刚好经过他的头顶,你能算出他的身高吗?(精确到0.01米) 米处跳,且绳子甩到最高处时刚好经过他的头顶,你能算出他的身高吗?(精确到0.01米) |
|
|
|
|
9.小敏身高1.70米,他站在什么位置时,跳绳甩到最高处时刚好经过他的头顶? |
|
|
|
|
10.议一议 现在有五个好朋友想站在线段CD上一起跳,他们的身高分别是1.72米、1.72米、1.80米、1.575米、1.575米,且人与人之间距离至少0.5米,你觉得不弯腰能同时跳吗?如果能,怎样跳?如果不能,请说明理由. |
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com