3．已知二次函数y＝x²-kx-15．当x＝5时，y＝0，求k．

2．已知二次函数y＝4x²+5x+1．求当y＝0时的x的值．

1．在长20cm，宽15cm的矩形木板的四角上各锯掉一个边长为xcm的正方形，写出余下木板的面积y(cm²)与正方形边长x(cm)之间的函数关系，并注明自变量的取值范围．

5．b和c是否可以为零？

　若b＝0，则y＝ax²+c；

　若c＝0，则y＝ax²+bx；

　若b＝c＝0，则y＝ax²．

　以上三种形式都是二次函数的特殊形式，而y＝ax²+bx+c是二次函数的一般形式．

4．为什么二次函数定义中要求a≠0？(若a＝0，ax²+bx+c就不是关于x的二次多项式了)

3．在y＝50x²+100x+50中， a＝50， b＝100， c＝50．

2．在y＝ax²+bx+c中自变量是x，它的取值范围是一切实数．但在实际问题中，自变量的取值范围是使实际问题有意义的值．

二次函数的定义：形如y＝ax²+bx+c(a≠0，a、b、c为常数)的函数叫做二次函数．

巩固对二次函数概念的理解：

1．强调“形如”，即由形来定义函数名称．二次函数即y是关于x的二次多项式．

例1 下列函数中哪些是二次函数？哪些不是二次函数？若是二次函数，指出a、b、c．

(1)y＝1-3x²；　　　　 (2)y＝x(x-5)；　　　　　　 (3)y＝3x(2-x)+3x²；

(4)y＝(x+2)(2-x)；　 (5)y＝x⁴+2x²+1．

解　 二次函数有(1)、(2)、(4)．

　　 (1)中　 ， ， ．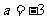

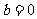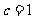(2)中 　，　 ＝ ， ．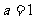

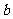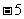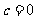(4)中 　， ， ．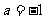

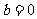例2　农机厂第一个月水泵的产量为50(台)第三个月的产量y(台)与月平均增长率x之间的函数关系如何表示？

解　函数关系式是y＝50(1+x)²，即y＝50x²+100x+50．

问题1中的函数关系式为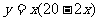 (0＜x＜10)；

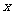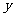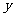问题2 设每件商品降价元，该商品每天的利润为元，是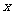的函数，则函数关系式为　　　 ．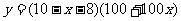

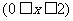得到的两个函数关系式有什么共同特点？这两个问题有什么共同特点？

概括：它们都是用自变量的二次多项式来表示的，问题都可归结为：自变量为何值时函数取得最大值？

二次函数的定义：形如y＝ax²+bx+c(a≠0，a、b、c为常数)的函数叫做二次函数(quadratic function)．