
6.下列函数关系中,可以看作二次函数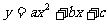 (
( )模型的是 ( )
)模型的是 ( )
A. 在一定的距离内汽车的行驶速度与行驶时间的关系
B. 我国人口年自然增长率为1%,这样我国人口总数随年份的变化关系
C. 竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D. 圆的周长与圆的半径之间的关系
[本课学习体会]
5.对于任意实数m,下列函数一定是二次函数的是 ( )
A. B.
B.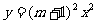 C.
C.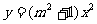 D.
D.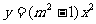
4. 用一根长为40 cm的铁丝围成一个半径为r的扇形,求扇形的面积y与它的半径x之间的函数关系式.这个函数是二次函数吗?请写出半径r的取值范围.
B组
3. 已知一个圆柱的高为27,底面半径为x,求圆柱的体积y与x的函数关系式.若圆柱的底面半径x为3,求此时的y.
2.
已知二次函数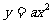 ,当x=3时,y= -5,当x= -5时,求y的值.
,当x=3时,y= -5,当x= -5时,求y的值.
1.
已知函数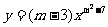 是二次函数,求m的值.
是二次函数,求m的值.
3.已知正方形的面积为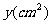 ,周长为x(cm).
,周长为x(cm).
(1)请写出y与x的函数关系式;
(2)判断y是否为x的二次函数.
[本课课外作业]
A组
2.当k为何值时,函数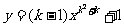 为二次函数?
为二次函数?
1.下列函数中,哪些是二次函数?
(1) (2)
(2)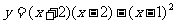
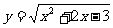
(3)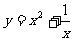 (4)
(4)
26.1 二次函数
[本课知识要点]
通过具体问题引入二次函数的概念,在解决问题的过程中体会二次函数的意义.
[MM及创新思维]
(1)正方形边长为a(cm),它的面积s(cm2)是多少?
(2)矩形的长是4厘米,宽是3厘米,如果将其长与宽都增加x厘米,则面积增加y平方厘米,试写出y与x的关系式.
请观察上面列出的两个式子,它们是不是函数?为什么?如果是函数,请你结合学习一次函数概念的经验,给它下个定义.
[实践与探索]
例1.
m取哪些值时,函数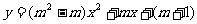 是以x为自变量的二次函数?
是以x为自变量的二次函数?
分析
若函数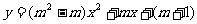 是二次函数,须满足的条件是:
是二次函数,须满足的条件是: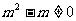 .
.
解
若函数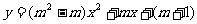 是二次函数,则
是二次函数,则
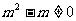 .
.
解得
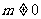 ,且
,且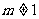 .
.
因此,当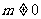 ,且
,且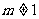 时,函数
时,函数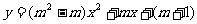 是二次函数.
是二次函数.
回顾与反思 形如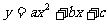 的函数只有在
的函数只有在 的条件下才是二次函数.
的条件下才是二次函数.
探索 若函数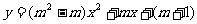 是以x为自变量的一次函数,则m取哪些值?
是以x为自变量的一次函数,则m取哪些值?
例2.写出下列各函数关系,并判断它们是什么类型的函数.
(1)写出正方体的表面积S(cm2)与正方体棱长a(cm)之间的函数关系;
(2)写出圆的面积y(cm2)与它的周长x(cm)之间的函数关系;
(3)某种储蓄的年利率是1.98%,存入10000元本金,若不计利息,求本息和y(元)与所存年数x之间的函数关系;
(4)菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.
解
(1)由题意,得 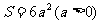 ,其中S是a的二次函数;
,其中S是a的二次函数;
(2)由题意,得 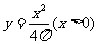 ,其中y是x的二次函数;
,其中y是x的二次函数;
(3)由题意,得 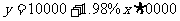 (x≥0且是正整数),
(x≥0且是正整数),
其中y是x的一次函数;
(4)由题意,得 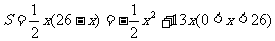 ,其中S是x的二次函数.
,其中S是x的二次函数.
例3.正方形铁片边长为15cm,在四个角上各剪去一个边长为x(cm)的小正方形,用余下的部分做成一个无盖的盒子.
(1)求盒子的表面积S(cm2)与小正方形边长x(cm)之间的函数关系式;
(2)当小正方形边长为3cm时,求盒子的表面积.
解
(1) ;
;
(2)当x=3cm时,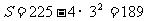 (cm2).
(cm2).
[当堂课内练习]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com