
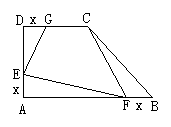
1.如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
5.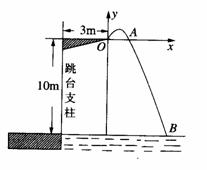 某跳水运动员在进行10m跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面
某跳水运动员在进行10m跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面 m,入水处距池边的距离为4m,同时运动员在距水面高度5m以前,必须完成规定的翻腾动作,并调整好入水姿势时,否则就会出现失误.
m,入水处距池边的距离为4m,同时运动员在距水面高度5m以前,必须完成规定的翻腾动作,并调整好入水姿势时,否则就会出现失误.
(1)求这条抛物线的函数关系式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为 m,问此次跳水会不会失误?并通过计算说明理由.
m,问此次跳水会不会失误?并通过计算说明理由.
[本课学习体会]
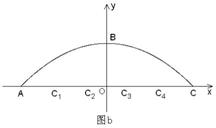
4.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图a)做成的立柱,为了计算所需不锈钢管立柱的总长度,设计人员利用图b所示的坐标系进行计算.
(1)求该抛物线的函数关系式;
(2)计算所需不锈钢管立柱的总长度.

0.25m处出手,问:球出手时,他跳离地面的高度是多少?
B组
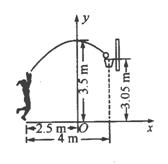
3.如图,一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮圈,已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线的函数关系式;
(2)该运动员身高1.8m,在这次跳投中,球在头顶上方
2.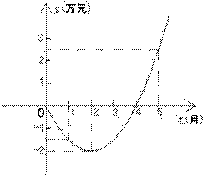 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程.
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程.
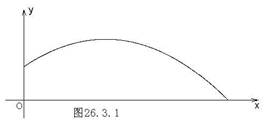
下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
 (3)求第8个月公司所获利润是多少万元?
(3)求第8个月公司所获利润是多少万元?
1.在一场足球赛中,一球员从球门正前方10米处将球踢起射向球门,当球飞行的水平距离是6米时,球到达最高点,此时球高3米,已知球门高2.44米,问能否射中球门?
2.在一场篮球赛中,队员甲跳起投篮,当球出手时离地高2.5米,与球圈中心的水平距离为7米,当球出手水平距离为4米时到达最大高度4米.设篮球运行轨迹为抛物线,球圈距地面3米,问此球是否投中?
[本课课外作业]
A组
1.在排球赛中,一队员站在边线发球,发球方向与边线垂直,球开始飞行时距地面1.9米,当球飞行距离为9米时达最大高度5.5米,已知球场长18米,问这样发球是否会直接把球打出边线?
26. 3 实践与探索(1)
[本课知识要点]
会结合二次函数的图象分析问题、解决问题,在运用中体会二次函数的实际意义.
[MM及创新思维]
生活中,我们常会遇到与二次函数及其图象有关的问题,比如在2004雅典奥运会的赛场上,很多项目,如跳水、铅球、篮球、足球、排球等都与二次函数及其图象息息相关.你知道二次函数在生活中的其它方面的运用吗?
[实践与探索]
 例1.如图26.3.1,一位运动员推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是
例1.如图26.3.1,一位运动员推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是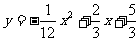 ,问此运动员把铅球推出多远?
,问此运动员把铅球推出多远?
解 如图,铅球落在x轴上,则y=0,
因此,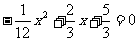 .
.
解方程,得 (不合题意,舍去).
(不合题意,舍去).
所以,此运动员把铅球推出了10米.
探索 此题根据已知条件求出了运动员把铅球推出的实际距离,如果创设另外一个问题情境:一个运动员推铅球,铅球刚出手时离地面 m,铅球落地点距铅球刚出手时相应的地面上的点10m,铅球运行中最高点离地面3m,已知铅球走过的路线是抛物线,求它的函数关系式.你能解决吗?试一试.
m,铅球落地点距铅球刚出手时相应的地面上的点10m,铅球运行中最高点离地面3m,已知铅球走过的路线是抛物线,求它的函数关系式.你能解决吗?试一试.
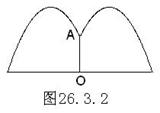
例2.如图26.3.2,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
 (1)若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?
(1)若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流最大高度应达多少米?(精确到0.1m)
 分析 这是一个运用抛物线的有关知识解决实际问题的应用题,首先必须将水流抛物线放在直角坐标系中,如图26.3.3,我们可以求出抛物线的函数关系式,再利用抛物线的性质即可解决问题.
分析 这是一个运用抛物线的有关知识解决实际问题的应用题,首先必须将水流抛物线放在直角坐标系中,如图26.3.3,我们可以求出抛物线的函数关系式,再利用抛物线的性质即可解决问题.
解 (1)以O为原点,OA为y轴建立坐标系.设抛物线顶点为B,水流落水与x轴交点为C(如图26.3.3).
由题意得,A(0,1.25),B(1,2.25),
因此,设抛物线为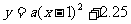 .
.
将A(0,1.25)代入上式,得 ,
,
解得
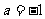
所以,抛物线的函数关系式为 .
.
当y=0时,解得 x=-0.5(不合题意,舍去),x=2.5,
所以C(2.5,0),即水池的半径至少要2.5m.
(2)由于喷出的抛物线形状与(1)相同,可设此抛物线为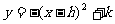 .
.
由抛物线过点(0,1.25)和(3.5,0),可求得h= -1.6,k=3.7.
所以,水流最大高度应达3.7m.
[当堂课内练习]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com