
2.如图,AB∥EF∥CD,CD=4,AB=9,若梯形CDEF与梯形EFAB相似,求EF的长.
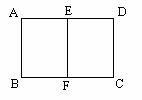 ※3.如图,一个矩形ABCD的长AD= a cm,宽AB= b cm,E、F分别是AD、BC的中点,连接E、F,所得新矩形ABFE与原矩形ABCD相似,求a:b的值. (
※3.如图,一个矩形ABCD的长AD= a cm,宽AB= b cm,E、F分别是AD、BC的中点,连接E、F,所得新矩形ABFE与原矩形ABCD相似,求a:b的值. (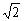 :1)
:1)
教学反思
1. 教材P41习题3、5、6.
5.已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是多少?
4.(选择题)下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个 B.4个 C.5个 D.6个
3.(选择题)△ABC与△DEF相似,且相似比是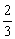 ,则△DEF 与△ABC与的相似比是( ).
,则△DEF 与△ABC与的相似比是( ).
A.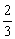 B.
B.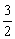 C.
C. D.
D.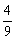
2.教材P41习题4.
1.教材P40练习2、3.
例1(补充)(选择题)下列说法正确的是( )
A.所有的平行四边形都相似 B.所有的矩形都相似
C.所有的菱形都相似 D.所有的正方形都相似
分析:A中平行四边形各角不一定对应相等,因此所有的平行四边形不一定都相似,故A错;B中矩形虽然各角都相等,但是各对应边的比不一定相等,因此所有的矩形不一定都相似,故B错;C中菱形虽然各对应边的比相等,但是各角不一定对应相等,因此所有的菱形不一定都相似,故C也错;D中任两个正方形的各角都相等,且各边都对应成比例,因此所有的正方形都相似,故D说法正确,因此此题应选D.
例2(教材P39例题).
分析:求相似多边形中的某些角的度数和某些线段的长,可根据相似多边形的对应角相等,对应边的比相等来解题,关键是找准对应角与对应边,从而列出正确的比例式.
解:略
例3(补充)
已知四边形ABCD与四边形A1B1C1D1相似,且A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD的各边的长.
分析:因为两个四边形相似,因此可根据相似多边形的对应边的比相等来解题.
解:∵ 四边形ABCD与四边形A1B1C1D1相似,
∴ AB:BC:CD:DA= A1B1:B1C1:C1D1:D1A1.
∵ A1B1:B1C1:C1D1:D1A1=7:8:11:14,
∴ AB:BC:CD:DA= 7:8:11:14.
设AB=7m,则BC=8m,CD=11m,DA=14m.
∵ 四边形ABCD的周长为40,
∴ 7m+8m+11m+14m=40.
∴ m=1.
∴ AB=7,则BC=8,CD=11,DA=14.
3.[结论]:
(1)相似多边形的特征:相似多边形的对应角相等,对应边的比相等.
反之,如果两个多边形的对应角相等,对应边的比相等,那么这两个多边形相似.
(2)相似比:相似多边形对应边的比称为相似比.
问题:相似比为1时,相似的两个图形有什么关系?
结论:相似比为1时,相似的两个图形全等,因此全等形是一种特殊的相似形.
2. 问题:对于图中两个相似的四边形,它们的对应角,对应边的比是否相等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com