2．下列图中的线段和线段的长度是否相等？用尺度量结果是否与你感觉一样？

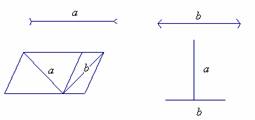
1．任意画一个四边形，分别用度量和剪拼的方法，求出该四边形的内角和的大小．你能说说理由吗？

2.如图，已知：AD＝AE，∠B＝∠C．求证：BE＝CD．

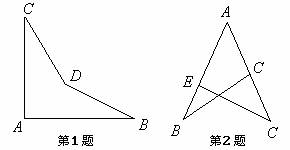
1.如图，是一个零件的形状，按规定应∠A＝90°，∠B和∠C应分别是30°和21°，检测工人量得∠BDC＝148°，就断定这个零件不合格，你能用学过的有关知识说明零件不合格的理由吗？

2.在推理过程中，不能只根据问题的某种相似性，生搬硬套，要正确运用定理公理等依据去证明几何图形的有关命题．

1.有些图形的性质可以通过观察和实验得到的，但仅仅通过观察和实验是不够的，必须要通过证明得；

2．变式：移动点A和点C的位置，可得一个五角星，求∠A+∠B+∠C+∠D+∠E的度数．

例1　如图，D是△ABC中BC边上的一点，E是AD上的一点，EB＝EC，∠ABE＝∠ACE．求证：△AEB≌△AEC．

分析　在已知条件中有求证三角形中的一对边和一对角，图中还有一对公共边，同学们很容易错将“边边角”当作“边角边”来证明，要正确应用公理和定理．

证明　因为　 　EB＝EC， 　　(已知)

　　　 所以　 　∠EBC＝∠ECB．　(等边对等角)

　 因为　　 ∠ABE＝∠ACE，　(已知)

　 　　所以　 ∠ABC＝∠ACB，　(等式性质)

　　　 所以　 AB＝AC．　　　(等角对等边)

　　　 在△AEB和△AEC中，AB＝AC，∠ABE＝∠ACE，BE＝CE．

　　　 所以　　 △AEB≌△AEC．　(边角边)

例2　如图，已知点A，C分别是线段BE、BD上的一点，连结AC，EC，AD．求证：∠CAD+∠ACE+∠B+∠D+∠E＝180°．

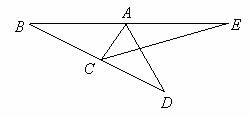
分析　利用三角形的外角的性质，把所证的5个角集中到一个三角形中，再用三角形内角和定理即可．

证明　因为∠BAC是△ACE的外角(如图)，

所以∠BAC＝∠ACE+∠E．(三角形的一个外角等于和它不相邻的两个内角的和)

同理∠BCA＝∠CAD+∠D．

又因为在△ABC中，∠BAC+∠ACB+∠B＝180°，(三角形内角和定理)

所以∠CAD+∠ACE+∠B+∠D+∠E＝180°．(等量代换)

说明　

1．换一个角度看，还可把5个角集中转移到平角∠BAE处；

我们已经学习了许多图形的性质，有些就是逻辑推理的最原始的依据--公理，还有一些是在公理的基础上用逻辑推理的方法去证明的，如：全等三角形的判定公理：边角边、角边角、边边边．除这些方法以外，同学们还有什么方法判断三角形全等？(角角边)我们一起来证明命题：有两个角及其中一个角的对边分别相等的两个三角形全等．

已知：△ABC和 △A′B′C′中，∠A＝∠A′，∠B＝∠B′，BC＝B′C′．

求证：△ABC≌ △A′B′C′．

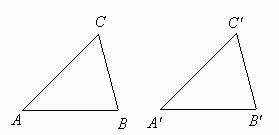
证明可让同学们自己探索完成．利用三角形内角和定理创造出角边角公理．

说明　这就是判定全等三角形的“角角边”定理：有两个角及其中一个角的对边分别相等的两个三角形全等．

　我们已经用逻辑推理的方法证明了三角形的内角和等于180度，同学们能否以这个定理为依据，来证明三角形的外角性质？哪位同学来说说三角形的外角具有什么性质？

求证：三角形的一个外角等于和它不相邻的两个内角的和．

已知：如图，∠CBD是△ABC的一个外角．

求证：∠CBD＝∠A+∠C．

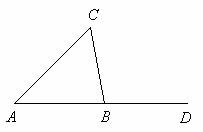
证明　因为∠A+∠ABC+∠C＝180°(三角形的内角和等于180°)，

　　所以∠A+∠C＝180°-∠ABC(等式的性质)．

　　又因为∠ABC+∠CBD＝180°(平角的定义)，

　　所以∠CBD＝180°-∠ABC(等式的性质)．

　　所以∠CBD＝∠A+∠C(等量代换)．

说明　1．这个性质常用作判断其他命题真假的依据，可作定理来使用；

2．可进一步得到∠CBD＞∠A，∠CBD＞∠C，即三角形的外角大于与它不相邻的任何一个内角．