
5.一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是21 °和32°.当检验工人量得的∠BDC的度数不等于多少度时,就可判定此零件不合格?

4.在甲、乙两地之间要修一条笔直的公路, 从甲地测得公路的走向是北偏东55°.如果甲、乙两地同时施工,那么在乙地公路应按北偏西多少度施工?
3.光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.

2.已知:如图所示,AB是⊙O的直线,PB切⊙O于B,OP∥AC,求证:PC是⊙O的切线.

1.已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD= BE.
求证:∠ABC=2∠C.

(1)已知一个多边形的内角和等于1080°,求这个多边形的边数.
(2)用三角形内角和定理,证明直角三角形的两个锐角之间的数量关系.
(3)利用“n边形的内角和等于(n-2)180°”这个结论,证明:任意多边形的外角和等于360°.
(1)探索几何图形性质的两种方法不是孤立的,实践为我们作出猜想提供了材料,推理证明为猜想的真实性提供保证;
(2)逻辑推理的依据有已知、定义、定理、公理、等式的性质、不等式的性质及等量代换等;
(3)注意证明的格式,每一步推理都必须有依据,证明的表述必须条理清晰.
例1 用逻辑推理的方法证明三角形的内角和是180度.
已知:△ABC. 求证:∠A+∠B+∠C=180°.

分析 回忆以前将三个内角拼在一起,发现三角形的三个内角的和等于180°,因此要设法将三个内角移在一个平角上,任作一个三角形ABC,延长AB到D,得平角ABD,过点B作BE∥AC,由平行线的性质把三个内角拼到点B处,证明过程如下:
证明 延长线段AB到D,过点B画BE∥AC.
因为BE∥AC(画图),
所以∠A=∠EBD(两直线平行,同位角相等),
∠C=∠CBE(两直线平行,内错角相等),
又因为∠EBD+∠CBE+∠ABC=180°(平角定义),
所以∠A+∠ABC+∠C=180°(等量代换).
得:三角形内角和定理:三角形的内角和等于180度.
说明 (1)为了证明的需要在原来的图中添画的线叫辅助线,辅助线常画成虚线;
(2)该定理的推理形式:因为 △ABC,所以∠A+∠B+∠C=180°(三角形内角和定理);
(3)该定理可以作为进一步推理的依据.利用三角形内角和定理,请同学们用逻辑推理的方法来说明(a)四边形内角和等于360°.(b)n边形的内角和等于(n-2)180°.
例2 如图,△ABC中,∠ABC的角平分线BD和∠ACB的角平分线CE相交于点O,且∠A=80°,求∠BOC的度数。
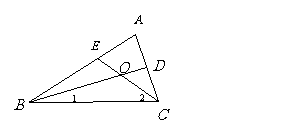
分析 在△ABC中,已知∠A的度数,利用三角形内角和定理,求∠ABC与∠ACB的和,又因为BD,CE分别平分∠ABC与∠ACB可得∠1与∠2的和,在△BOC中由三角形内角和定理可求∠BOC的度数.
解 在△ABC中,∠ABC+∠ACB=180°-∠A=180°-80°=100°(三角形内角和定理)
因为 ∠1=1/2∠ABC,∠2=1/2∠ACB(角平分线定义),
所以 ∠1+∠2=1/2(∠ABC+∠ACB)=100°/2=50° (等式性质),
在 △BOC中,∠BOC=180°-(∠1+∠2)=180°-50°=130° (三角形内角和定理).
2.逻辑推理需要依据,依据包括公理,等式与不等式的有关性质以及等量代换,定理.
公理:(1)一条直线截两条平行直线所得的同位角相等;
(2)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
(3)如果两个三角形的两边及其夹角(或两角及其夹边,或三边)分别对应相等,那么这两个三角形全等;
(4)全等三角形的对应边、对应角相等.
定理:在公理与依据的基础上,用逻辑推理的方法去证明几何图形的有关命题,并将证得的可以作为进一步推理依据的真命题称为定理.
我们需要将证明的每一步的依据要写在所得到的结论后面.
1.探索几何图形的性质时,常常采用看一看,画一画,比一比,量一量,算一算,想一想,猜一猜等方法得出结论,并在实验操作中对结论作出解释,这是研究几何图形性质的一种基本方法.但有时视觉上的错觉会误导我们,凭直觉的方法研究几何图形所得出的结论不一定正确,所以我们要学习用逻辑推理的方法(既证明)去探索图形的性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com