7、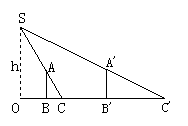为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB^‘),再把竹竿竖立在地面上, 测得竹竿的影长(B^‘C^‘)为1.8米,求路灯离地面的高度.

答案：1、30m　 2、70米　　 3、5.6米　　 4、5.6米

6、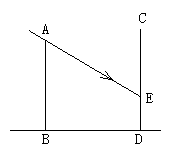如图,甲楼AB高18米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1: 　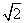,已知两楼相距20米,那么甲楼的影子落在乙楼上有多高?

5、如图，在4×4方格纸中，△ABC和△DEF的顶点都在边长为1的小正方形

的顶点上，判断△ABC和△DEF是否相似？并证明你的结论.

4、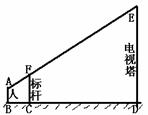如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，求电视塔的高ED.

3、(06湖州)为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据《科学》中光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子放在离树底(B)8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树(AB)的高度约为________米(精确到0.1米).

2、如图，在河两岸分别有A、B两村，现测得A、B、D在一条直线上，A、C、E在一条直线上，BC//DE，DE=90米，BC=70米，BD=20米.则A、B两村间的距离为　　　　　 .

1、在阳光下，身高1.68m的小强在地面上的影长为2m，在同一时刻，测得学校的旗杆在地面上的影长为18m．则旗杆的高度为　　　　　　　 (精确到0.1m)．

27.2.2相似三角形应用举例

3．小R、小D、小H在一起研究相似三角形，分别得到三个命题：

　　 (1)两个相似三角形，如果它们的周长相等，那么这两个三角形全等；

　　 (2)两个相似三角形，如果有两组边长相等，那么这两个三角形全等；

　　 (3)不等边△ABC的边长为a、b、c，那么以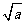、、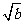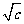为边长的△A′B′C一定不能与△ABC相似．

　　 请你判定一下，这三个命题中，哪些是真命题？说说你的理由．

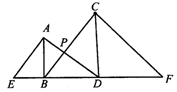
2．如图，运河边上移栽了两棵老树AB、CD，它们相距20m，分别自两树上高出地面3m、4m的A、C处，向两侧地面上的点E和D、B和F处用绳索拉紧，以固定老树，那么绳索AD与BC的交点P离地面的高度为多少米？