(一)创设情境，提出问题

在哈密市环城路的建设施工中，曾遇到这样一个实际问题：

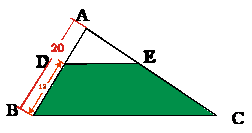
由于马路拓宽，有一个面积是100平方米、周长80米的三角形的绿化地被削去了一个角，变成了一块梯形绿地，原绿化地的一边AB的长由原来的20米缩短成12米(如图所示).为了保证哈密的绿化建设，市政府规定：因为种种原因而失去的绿地面积必须等面积补回.这样就引出了一个问题：这块失去的面积到底有多大？它的周长是多少？

你能够将上面生活中的实际问题转化为数学问题吗？

(通过对课本例题进行“再创造”，以建设环城路为背景，引出数学问题.既尊重课本内容又符合加强数学与现实联系的要求.)

重点：相似三角形的周长比、面积比与相似比的关系的探究与证明.

难点：相似三角形的周长比、面积比与相似比的关系的应用.

3．在学习过程中，进一步改善独立思考、合作学习、自主评价等学习品质.

2．在动手参与解决身边实际问题的过程中，增强主动探索、发现数学知识的意识，提高观察、归纳能力，应用数学知识解决生活中实际问题的能力.

1、初步掌握相似三角形的周长比、面积比与相似比的关系以及关于它们之间关系的两条定理的证明方法，并会运用定理进行有关简单的计算.

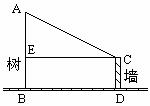
3．　 小明想利用树影测量树高，他在某一时刻测得长为1m的竹竿影长0.9m，但当他马上测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上，如图，他先测得留在墙上的影高1.2m，又测得地面部分的影长2.7m，他求得的树高是多少？

教学反思

2．　 如图，小明在打网球时，使球恰好能打过网，而且落在离网5米的位置上，求球拍击球的高度h．(设网球是直线运动)

1．　 教材P51.练习1和练习2．

2．　 小明要测量一座古塔的高度，从距他2米的一小块积水处C看到塔顶的倒影，已知小明的眼部离地面的高度DE是1.5米，塔底中心B到积水处C的距离是40米.求塔高?

1．　 在同一时刻物体的高度与它的影长成正比例．在某一时刻，有人测得一高为1.8米的竹竿的影长为3米，某一高楼的影长为60米，那么高楼的高度是多少米?