
为了培养学生的逻辑思维能力、自学能力和自己发现问题---提出问题----解决问题的学习方法,在教学上我采用“实验探究、以新带旧、精心设疑、变式训练”等方法,充分调动学生的积极性,使学生始终处于最佳的思维状态之中,激发学生的兴趣.
为了充分调动学生学习的积极性,使空间与图形中的几何问题上得生动、有趣和高效,教学中,我引导学生从实验入手,让学生经历动手实验--观察--思考--猜想--归纳探究的学习过程,总结出两个相似三角形的周长比、面积比与相似比的关系。
在教学中采用投影、计算机等电教手段,增大教学的容量和直观性,以提高教学效率和教学质量。
3、 教学重点及难点
因为相似三角形的周长比、面积比与相似比的关系是解决与相似三角形有关问题的重要依据,也是研究相似多边形性质的基础,因此,它是本节教材的重点。学生应用数学知识解决实际问题,需要具备一定的综合能力,这对大部分学生有一定的难度,因此,将相似三角形的周长比、面积比与相似比的关系的应用确定为本节课的难点。通过学生动手操作及合作交流,进行探究相关问题来突出重点,突破难点。
2、 教学目标的确定
1) 通过探究相似三角形的周长比、面积比与相似比的关系,使学生掌握相似三角形的周长比等于相似比,面积比等于相似比的平方。
2) 在动手参与解决身边实际问题的过程中,增强主动探索,发现数学知识的意识,提高观察、归纳能力,应用数学知识解决生活中实际问题的能力。
3) 在学习过程中,培养学生独立思考、合作学习、自主评价的能力,渗透数学当中的建模思想、转化思想。
1、教材所处的地位及作用
“相似三角形的周长与面积”是在学完相似三角形的定义及判定的基础上,来研究相似三角形的特征,以完成对相似三角形的全面研究,它是全等三角形性质的拓展,也是解决有关实际问题的重要工具,因此,这节课无论在知识上,还是对学生能力的培养上,都起着十分重要的作用。
(六)课后反思:
(五)分层作业,着眼发展
过点E作EF//AB,EF交BC于点F,其他条件不变,则 的面积等于多少?平行四边形DBFE面积为多少?
的面积等于多少?平行四边形DBFE面积为多少?
(2)猜想相似多边形的周长比,面积比与相似比有怎样的关系?
(作业的布置,帮助学生对知识的保持和迁移,尊重学生的个体差异满足多样化的学习需要,使不同层次的学生有不同的收获.)
(四)小结反思, 自主评价
1. 知识技能部分的小结:
相似三角形的周长比、面积比与相似比的关系;两条有关定理的证明思路与证明方法;定理的运用(进行有关简单的计算).
2.自主评价:
如:对网格图上的两个格点三角形相似的认识;对运用定理解决问题的注意点的反思性总结;对自己及同伴在课堂上数学学习表现的评价;提出自己的困惑与不解,或进行质疑等.
3. 教师根据学生自主评价情况作适当的点评.
教师根据学生自主评价情况作适当的点评.
(三)运用性质,熟悉新知
1.已知两个三角形相似,根据下列数据填表:
|
相似比 |
2 |
|
|
1/3 |
|
|
|
周长比 |
|
0.01 |
10 |
|
|
|
|
面积比 |
|
|
|
|
10000 |
0.0001 |
2. 实际问题的解决
实际问题的解决
如图,已知,在△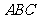 中,
中,
DE∥BC,AB=20m,BD=12m, △ 的周长为80m,面积为100m2,求:△
的周长为80m,面积为100m2,求:△ 的周长和面积.
的周长和面积.
(通过探索、论证,到运用解决实际问题,一方面学生摸索到了从已知到未知的研究方法,另一方面又感受到了数学来源于生活又服务于生活.)
3.引申
分别连结CD和BE交于点G,
求:(1)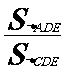
(2) ,
,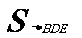
(3)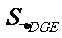 ,
,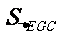 ,
, ,
, .
.
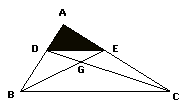
(对引例的变式是培养学生多层次、多角度思维能力的一种较好形式.复杂图形中观察基本图形对学生来说有一定的难度,教师借助于多媒体的力量,采用图形的闪烁,色彩的变化等手段,突出基本图形,突破难点.)
(二)自主探究,发现新知
1.分组探究活动
完成下列实验报告单
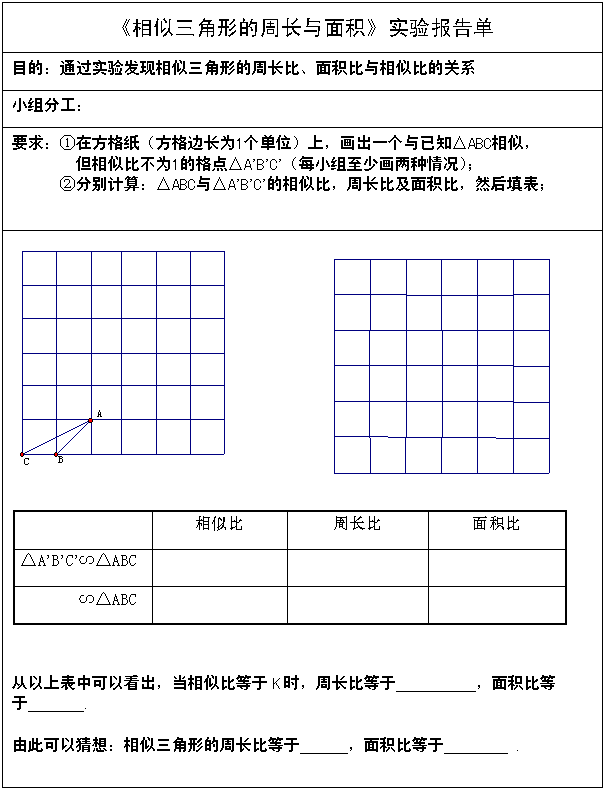
(学生经历动手实验 - 观察-思考-归纳-发现的学习过程,分别总结两个相似三角形的周长比与相似比的关系,面积比与相似比的关系.注重学生动手实验、探索过程,并利用小组合作方式,培养学生的合作意识.)
附件1:通过上一节课完成的实验报告单,让学生回答实验报告单中的思考作业.
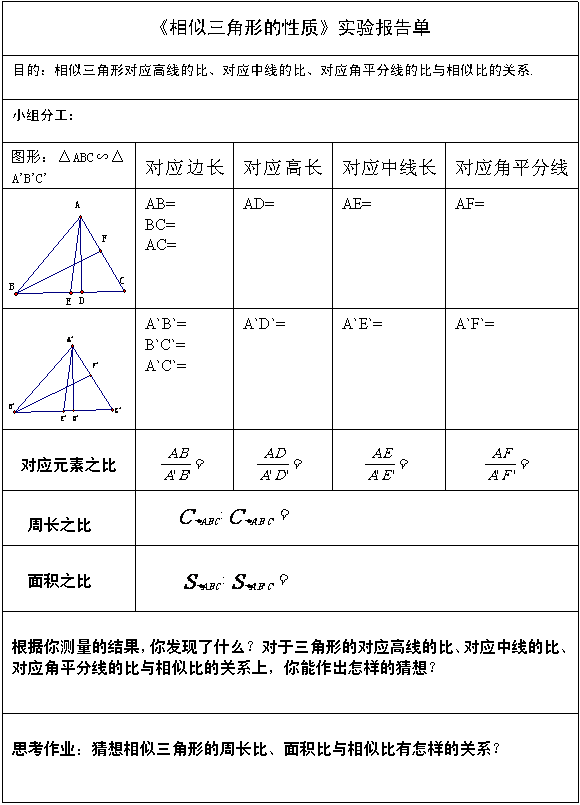
(对上一节课实验报告单的再次利用,让学生发现,通过上一节课的动手测量和本节课在网格图中的动手计算得出相似三角形的周长比,面积比与相似比关系的猜想完全一致,再次证明学生猜想的正确性.)
猜测得到命题:相似三角形的周长比等于相似比.
相似三角形的面积比等于相似比的平方.
2.证明所得命题
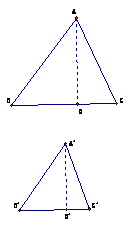 已知:如图,△
已知:如图,△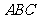 ∽△
∽△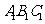 ,相似比为k,
,相似比为k,
求证: 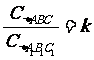 ,
, .
.
 证明:
证明:
△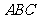 ∽△
∽△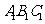


 .
.
分别过A、A’作△ABC, △A’B’C’ 的高AD,A’D’
 △
△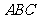 ∽△
∽△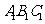
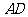 、
、 分别是△
分别是△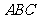 、△
、△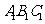 的高
的高

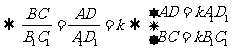
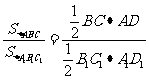

 .
.
(基于对网格具有支架作用的认识,同时考虑到学生学习相似三角形的判定时对网格图已有接触、比较熟悉,所以探究活动选择网格图上的格点三角形进行研究,便于学生进行边长、周长、面积的计算.探究活动①的设计,复旧育新,不但复习了相似三角形的判定,同时为新知识的获取创造条件.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com