2．相似三角形面积的比等于_________；相似多边形面积的比等于_________．

1．相似三角形周长的比等于________，相似多边形周长的比等于_______，相似三角形对应高的比等于________，相似三角形对应中线的比等于________，相似三角形的对应角平分线的比等于________．

7.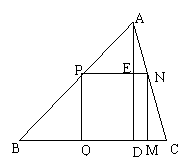如图，△ABC是一块锐角三角形余料，边BC=120mm， 高AD=80mm， 要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上，

(1)若这个矩形是正方形，那么边长是多少？

(2)若这个矩形的长是宽的2倍，则边长是多少？

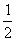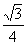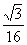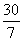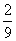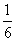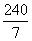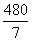答案：1、8cm　　 2、A　 3、B　 4、(1)相似.　 (2)a² a²　 (3)面积之比的平方等于相似比　 5、(1)x=s　 (2)　 6 、　　 7、(1)48 mm (2)宽是mm，长mm.

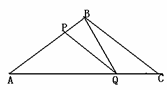
6.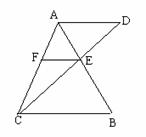在△ABC中，AE∶EB=1 ∶2，EF∥BC，AD∥BC交CE的延长线于D，求S_△AEF∶S_△BCE的值.

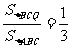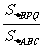5.如图，在ΔABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x.(1)当x为何值时，PQ∥BC？(2)当，求的值；

3.如图，这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米，桌面离地面1米. 若灯泡离地面3米，则地面上阴影部分的面积为　　　　　　　　　　　　　　　　　 (　 -)

A.、0.36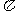米²　 B、0.81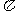米²　　 C、2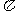米²　　　　　 D、3.24米²

4.如图，分别取等边三角形ABC各边的中点D、E、F，得△DEF.若△ABC的边长为a.

(1)△DEF与△ABC相似吗？如果相似，相似比是多少？

(2)分别求出这两个三角形的面积.

(3)这两个三角形的面积比与边长之比有什么关系吗？

2.等腰三角形ABC和DEF相似，其相似比为3：4，则它们底边上对应高线的比为(　 )

A、3：4　　　　 B、4：3　　　　 C、1：2　　　　　 D、2：1

1.若△ABC∽△DEF,△ABC的面积为81cm²,△DEF的面积为36cm²,且AB=12cm,则

DE=　　　　 cm

27.2.3相似三角形的周长与面积

　(消音)本节课的引入，是通过改变教材例题的呈现形式，以哈密市环城路建设为背景，提出数学问题。这样的设计，既可以调动学生的学习热情与积极性，又可以使学生认识到现实生活中处处有数学，提高学生应用数学的意识。

(消音)为了让学生亲身体验知识发现产生的过程,我借鉴物理中实验报告单的形式,设计了<<相似三角形的周长与面积>>实验报告单,其目的是:让学生通过探究试验,发现相似三角形的周长比、面积比与相似比的关系。对网格图上的格点三角形进行探究，主要考虑网格有支架作用，便于学生进行边长、周长、面积的计算。另外对于网格图学生在相似三角形的判定中已有接触，比较熟悉。这部分注重学生的动手实验、探究过程，并利用小组合作方式，培养学生的合作意识。

(消音)对上一节课实验报告单的再次利用,让学生发现,通过上一节课的动手测量和本节课在网格图中的动手计算得出相似三角形的周长比,面积比与相似比关系的猜想完全一致,再次证明学生猜想的正确性.

(消音)在得出定理后，及时进行由浅入深、由易到难的思维训练。通过探究、论证，到运用解决实际问题，一方面学生摸索到了从已知到未知的研究方法，另一方面又感受到了数学来源于生活又服务于生活。

(消音)对引例的变式训练是培养学生多层次、多角度思维能力的一种较好形式,复杂图形中观察基本图形对学生来说有一定的难度，我借助于多媒体的力量，采用色彩的变化，突出基本图形，突破难点。

(消音)小结部分，用三个问题引导学生小结反思与自主评价。首先让学生归纳刚获得的知识和技能，再引导学生回顾知识发现的过程,使学生对已有知识进行反思,再次明确重、难点,让学生获得解决一类问题的方法.

(消音)分层作业的布置,帮助学生对知识的保持和迁移,尊重学生的个体差异满足多样化的学习需要,使不同层次的学生有不同的收获.同时,选做题可引导学生进行自学探究,为下一节课的教学做好准备.

课后反思：