
6.已知二次函数y=mx2+(m−1)x+m−1的图象有最低点,且最低点的纵坐标是零,则m=_______.
5.二次函数y=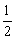 x2+3x+
x2+3x+ 的图象是由函数y=
的图象是由函数y=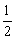 x2的图象先向_____平移____个单位,再向_____平移_____个单位得到的.
x2的图象先向_____平移____个单位,再向_____平移_____个单位得到的.
4.如果函数y=(k−3)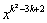 +kx+1是二次函数,则k的值一定是_______.
+kx+1是二次函数,则k的值一定是_______.
3.二次函数y=ax2+bx+c中,a>0,b<0,c=0,则其图象的顶点是在第_____象限.
2.二次函数y=2x2+bx+c的顶点坐标是(1,−2),则b=_____,c=_____.
1.二次函数y=3x2−2x+1的图象是开口方向_______,顶点是________, 对称轴是__________.
27.2.3相似三角形的周长与面积

|
教 学 目 标 |
知识技能 |
理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方. |
|
数学思考 |
以问题的形式,创设一个有利于学生动手和探究的情境,达到掌握相似三角形周长的比等于相似比、面积比等于相似比的平方的目的. |
|
|
解决问题 |
学生动手和探究达到掌握相似三角形周长的比等于相似比、面积比等于相似比的平方的目的. |
|
|
情感态度 |
培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值. |
|
|
重点 |
理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方. |
|
|
难点 |
探索相似多边形周长的比等于相似比、面积比等于相似比的平方. |

|
教学过程 |
设计意图说明 |
|
新课引入: 复习:相似多边形对应边、对应角的性质;相似比的定义 |
以旧引新,帮助学生建立新旧知识间的联系. |
|
提出问题: 如果两个三角形相似,它们的周长之间什么关系?两个相似多边形呢? (小组讨论) 如果△ABC∽△A'B'C',相似比为k,那么  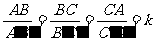  AB=kA′B AB=kA′B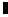 ,BC=kB ,BC=kB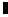 C C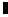 ,CA=kC ,CA=kC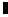 A A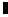   可以得到 相似三角形周长的比等于相似比 类似的方法还可以得出 相似多边形周长的比等于相似比 延伸问题: 探究: (1) 如图27.2-11⑴,∆ABC∽∆ A'B'C',相似比为k1 ,它们的面积比是多少? 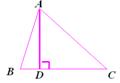 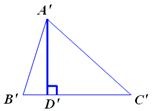
图27.2-11⑴ 分析:如图27.2-11,分别作出∆ABC和∆ A'B'C'的高AD和A'D'. ∠ADB=∠A'D'B'=900又∠B=∠B' ∆ABD∽∆A'B'D' 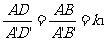 (在此得出相似三角形对应高的比等于相似比) (在此得出相似三角形对应高的比等于相似比)  =k12 =k12可以得到:相似三角形面积比等于相似比的平方 相似三角形对应中线的比,对应角平分线的比都等于相似比吗? (2)如图图27.2-11(2),四边形ABCD相似于四边形A'B'C'D',相似比为k2,它们的面积比是多少? 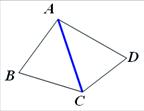  图27.2-11(2) ∵ 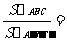  k22
k22∴ 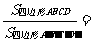  k22 k22相似多边形面积比等于相似比的平方 应用新知: 例6:如图27.2-12,在∆ABC和∆DEF中,AB=2DE,AC=2DF, ∠A=∠D,∆ABC的周长是24,面积是48,求 ∆DEF的周长和面积. 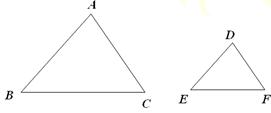 分析: ∆ABC和∆DEF中,AB=2DE,AC=2DF ∴ 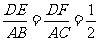 又∠A=∠D 又∠A=∠D∴∆ABC∽∆DEF,相似比为 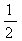 ∆DEF的周长= 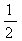 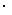 24=12,面积= 24=12,面积= 2 2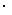 48=12. 48=12. |
让学生经历从特殊到一般的过程,体会有限数学归纳法的魅力,学生以小组讨论的形式开展学习有利于丰富学生的探究经验. 让学生经历从“相似三角形周长的比与相似比的关系到相似三角形面积比与相似比的关系”的过程,体会它们之间的形式雷同性与认知结构雷同性. 提出问题,留给学生独立探究的空间. 让学生再次经历从特殊到一般的过程,进一步体验有限数学归纳法的魅力. 让学生了解运用“相似三角形周长的比等于相似比、面积比等于相似比的平方”的常见解题思路. |
|
运用提高: 1. P54练习题1 2. P54练习题2 |
让学生在练习中熟悉利用相似三角形周长的比等于相似比、面积比等于相似比的平方,解决简单的问题. |
|
课堂小结:说说你在本节课的收获. |
让学生及时回顾整理本节课所学的知识. |
|
布置作业:(附练习卷) 1. 必做题:A卷 2. 选做题:B卷 |
分层次布置作业,让不同的学生在本节课中都有收获. |
设计思想:
本节课主要是让学生理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,通过探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想,学会应用相似三角形周长的比等于相似比、面积比等于相似比的平方来解决简单的问题.因此本教学设计突出了“相似比 相似三角形周长的比
相似三角形周长的比 相似多边形周长的比”、“相似比
相似多边形周长的比”、“相似比 相似三角形面积的比
相似三角形面积的比 相似多边形面积的比”等一系列从特殊到一般的过程,以让学生深刻体验到有限数学归纳法的魅力.
相似多边形面积的比”等一系列从特殊到一般的过程,以让学生深刻体验到有限数学归纳法的魅力.
4.下列图形中,图①是边长为1的阴影正三角形,连结它的各边中点,挖去中间的三角形得到图②,再分别连结剩下的每个阴影三角形各边中点,挖去中间的三角形得到图③.再用同样的方法得到图④.
(1)请你求出图④中阴影部分的面积;
(2)若再用同样的方法继续下去,试猜想图n中阴影部分的面积.
(3)试说出图⑤中三角形的个数.

3.某校准备耗资1600元,在一块上、下两底分别为10m、20m的梯形ABCD空地上种植花木,AD∥BC.
(1)如果在△AMD和△BMC地上种植太阳花,单价为8元/m2,将△AMD地上种满花,共花了160元,请计算种满△BMC地上所需的费用;
(2)如果其余地上要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m2和10元/m2,应选择哪种花木,刚好用完准备的1600元资金?

2.如图,△ABC的面积为16,AB=4,D为AB上任一点,F为BD的中点,DE∥BC,FG∥BC,分别交AC于E、G,设AD=x.
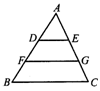 (1)把△ADE的面积S1用含x的代数式表示;
(1)把△ADE的面积S1用含x的代数式表示;
(2)把梯形DFGE的面积S2,用含x的代数式表示.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com