
2.任给一些不同的实数k,得到不同的抛物线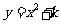 ,当k取0,
,当k取0, 时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最低点.其中判断正确的是
.
时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最低点.其中判断正确的是
.
1.二次函数
 中,若当x取x1、x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值等于
.
中,若当x取x1、x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值等于
.
6.已知抛物线y=2 x2–1上有两点(x1,y1) ,(x2,y2 )且x1<x2<0,则y1 y2 (填“<”或“>”)
5.将抛物线 向下平移2个单位得到的抛物线的解析式为
,再向上平移3个单位得到的抛物线的解析式为
,并分别写出这两个函数的顶点坐标
、
.
向下平移2个单位得到的抛物线的解析式为
,再向上平移3个单位得到的抛物线的解析式为
,并分别写出这两个函数的顶点坐标
、
.
4.对于函数y=-x2+1的图象,顶点是 ,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 .
3.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向 C.顶点 D.形状
2.抛物线 的开口 ,对称轴是 ,顶点坐标是
,当x 时, y随x的增大而增大, 当x 时, y随x的增大而减小.
的开口 ,对称轴是 ,顶点坐标是
,当x 时, y随x的增大而增大, 当x 时, y随x的增大而减小.
1.把抛物线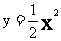 向下平移2个单位,可以得到抛物线
,再向上平移5个单位,可以得到抛物线
;
向下平移2个单位,可以得到抛物线
,再向上平移5个单位,可以得到抛物线
;
二次函数y=ax2与y=ax2+c的图象的关系:
二次函数y=ax2+c的图象可以由y=ax2 的图象上下平移得到:
当c > 0 时,向上平移|c|个单位得到.
当c < 0 时,向下平移|c|个单位得到.
|
函数 |
开口方向 |
对称轴 |
顶点坐标 |
|
y=ax2 |
|
|
|
|
y=ax2+c |
|
|
|
活动1 在同一平面直角坐标系画出函数y=x2、y=x2+1与 y=x2-1的图象.
解:(1)列表:
|
x |
… |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
|
y=x2 |
… |
|
|
|
|
|
|
|
… |
|
y=x2+1 |
… |
|
|
|
|
|
|
|
… |
|
y=x2-1 |
… |
|
|
|
|
|
|
|
… |
(2)描点:用表里各组对应值作为点的坐标,在平面直角坐标系中描点.
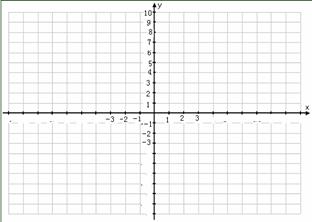
(3)连线:用光滑曲线顺次连接各点,得到函数y=x2、y=x2+1与 y=x2-1的图象.
观察图象回答下列问题:
(1)
|
函数 |
开口方向 |
对称轴 |
顶点坐标 |
|
y=x2 |
|
|
|
|
y=x2+1 |
|
|
|
|
y=x2-1 |
|
|
|
(2)抛物线 y=x2+1是由抛物线y=x2沿y轴向 平移 个单位长度得到的;
抛物线y=x2-1是由抛物线y=x2沿y轴向 平移 个单位长度得到的;
(3)你认为是什么决定了会这样平移?
活动2
在同一直角坐标系内画出下列二次函数的图象:
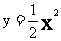 、
、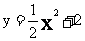 、
、 ,观察三条抛物线的相互关系,并分别指出它们的开口方
,观察三条抛物线的相互关系,并分别指出它们的开口方
向及对称轴、顶点坐标.你能说出抛物线 的开口方向及对称轴、顶点坐标吗?
的开口方向及对称轴、顶点坐标吗?
解:(1)列表:
(2)描点:用表里各组对应值作为点的坐标,在平面直角坐标系中描点.
 (3)连线:用光滑曲线顺次连接各点,得到函数
(3)连线:用光滑曲线顺次连接各点,得到函数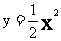 、
、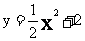 、
、 的图象.
的图象.
观察图象回答下列问题
(1)
|
函数 |
开口方向 |
对称轴 |
顶点坐标 |
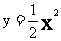 |
|
|
|
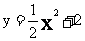 |
|
|
|
 |
|
|
|
(2)抛物线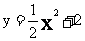 是由抛物线
是由抛物线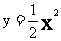 沿y轴向 平移 个单位长度得到的;
沿y轴向 平移 个单位长度得到的;
抛物线 是由抛物线
是由抛物线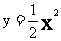 沿y轴向 平移 个单位长度得到的;
沿y轴向 平移 个单位长度得到的;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com