
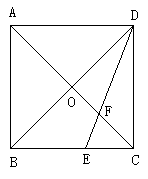
5. 如图3,正方形ABCD的对角线AC、BD相交于点O,E是BC的中点,DE交AC于F,若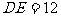 ,则EF等于( )
,则EF等于( )
A. 8 B. 6 C. 4 D. 3
2. 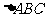 中,D是AB上的一点,在AC上取一点E,使得以A、D、E为顶点的三角形与
中,D是AB上的一点,在AC上取一点E,使得以A、D、E为顶点的三角形与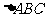 相似,则这样的点的个数最多是( )
相似,则这样的点的个数最多是( )
A. 0 B. 1 C. 2 D. 无数
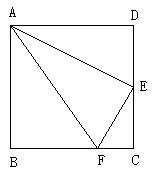 3. 如图1,正方形ABCD中,E是CD的中点,
3. 如图1,正方形ABCD中,E是CD的中点, ,下面得出六个结论:(1)
,下面得出六个结论:(1) ;(2)
;(2) ;(3)
;(3)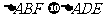 ;(4)
;(4) ;(5)
;(5)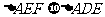 ;(6)
;(6)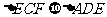 。其中正确的个数是( )
。其中正确的个数是( )
A. 1个 B. 3个 C. 4个 D. 5个
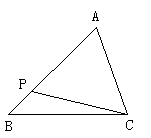 4. (哈尔滨市,2002)已知,如图2,
4. (哈尔滨市,2002)已知,如图2,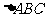 中,P为AB上一点,在下列四个条件中:(1)
中,P为AB上一点,在下列四个条件中:(1)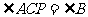 ;(2)
;(2)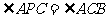 ;(3)
;(3)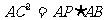 ;(4)
;(4)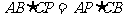 。能满足
。能满足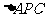 和
和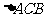 相似的条件是( )
相似的条件是( )
 A. (1)(2)(4) B. (1)(3)(4)
A. (1)(2)(4) B. (1)(3)(4)
C. (2)(3)(4) D. (1)(2)(3)
图2
1. 在直角三角形中,两直角边分别为3、4,则这个三角形的斜边与斜边上的高的比是( )
A. 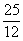 B.
B.
 C.
C.
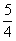 D.
D.

(二)三角形相似的判定方法
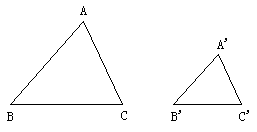 (1)定义法:对应角相等,对应边成比例的三角形相似。
(1)定义法:对应角相等,对应边成比例的三角形相似。
如图,若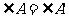 ,
,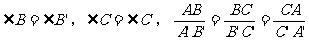 ,
,
则 。
。
与三个角对应相等,三条边对应相等,两个三角形全等类似,定义法在计算和证明中一般用得较少。
(2)三角形相似的判定定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
推理格式:如图
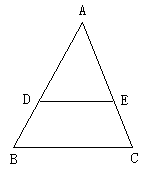
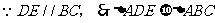
图2
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
推理格式:如图,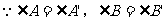 ,
,
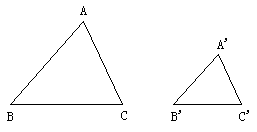
 。
。
简单地说:两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
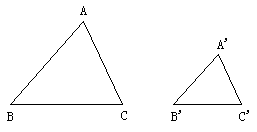 推理格式:如图,
推理格式:如图,
 ,且
,且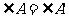

可简单说成:两边对应成比例且夹角相等,则两三角形相似。
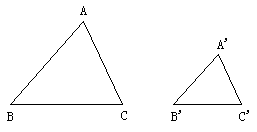 (5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
推理格式:如图5,
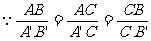 ,
,

简单地说:三边对应成比例,则两三角形相似。
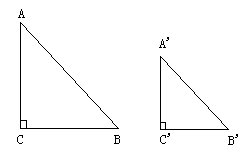 (6)直角三角形相似的判定定理:
(6)直角三角形相似的判定定理:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
推理格式:如图6
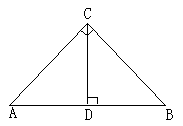 在
在 和
和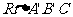 中,
中,
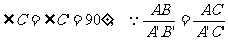

推论:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似(如图)。
说明:灵活运用相似三角形的判定方法解决相关问题,其关键是确定相似三角形,通常按下列思路来分析:
1. 有平行线(有时要构造平行线)时,可选择平行法判定三角形相似。
2. 若已经有一组角相等,可再找另一组角相等,运用判定定理1;或再证明夹这组角的两边对应成比例,运用判定定理2。
3. 若已知两条对应边成比例,可找夹角相等,运用判定定理2。
4. 若是两个直角三角形,可找一对锐角相等或夹直角的两直角边对应成比例,或应用斜边、直角边对应成比例来判定相似。
5. 利用相似三角形的传递性证相似,如:若 、
、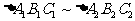 ,则
,则 。
。
6. 注意:仅两边成比例,一对角相等的三角形不一定相似。
[典型例题]
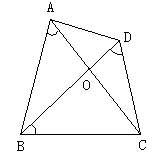 例1. 如图8,四边形ABCD的对角线相交于点O,
例1. 如图8,四边形ABCD的对角线相交于点O, 。求证:
。求证: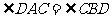 。
。
分析:欲证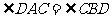 ,可寻求它们所在的三角形
,可寻求它们所在的三角形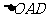 与
与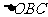 相似,
相似,
而 ,故只需证
,故只需证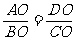 ,
,
由已知可得 ,从而有
,从而有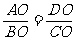 成立。
成立。
证明: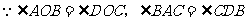
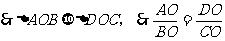
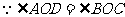

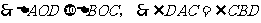
说明:由于相似三角形的对应角相等,所以经常运用此法证明角的相等。
例2. 如图9,平行四边形ABCD中,E是AB延长线上一点,连结DE,交AC于G,交BC于F,那么图中相似三角形(不含全等三角形)共有( )对。
A. 6 B. 5 C. 4 D. 3
分析:找相似形一找平行线、二找角相等、三找线段成比例,本题只能从前两方面入手。
解: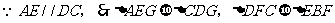

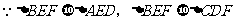
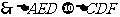 共有5对,选B。
共有5对,选B。
例3. 已知:如图10, ,
,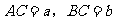 ,
,
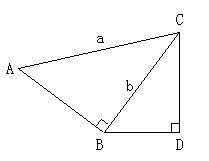 (1)当BD与a、b之间满足怎样的关系时,
(1)当BD与a、b之间满足怎样的关系时, ?
?
(2)当BD与a、b之间满足怎样的关系时, ?
?
(3)当BD与a,b之间满足怎样的关系时,这两个三角形相似?
解:(1)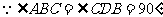
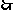 当
当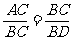 时,
时,
即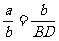 时,
时,
故当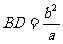 时,
时,
(2)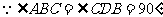 ,
,
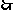 当
当 时,
时,
即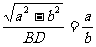 时,
时,
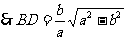
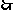 当
当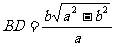 时,
时,
(3)综合(1),(2)可知:
当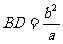 或
或 时这两个三角形相似。
时这两个三角形相似。
[模拟试题](答题时间:20分钟)
(一)复习
1. 相似三角形的定义:对应角相等,对应边成比例的三角形,叫做相似三角形。
2. 注意:
(1)定义中对应角相等,对应边成比例,是指3组对应角分别相等,三组对应边成比例。
(2) 读作
读作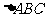 相似于
相似于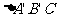 ,与全等三角形一样,表示对应顶点的字母应写在对应位置上。
,与全等三角形一样,表示对应顶点的字母应写在对应位置上。
(3)所谓相似三角形是指两个三角形形状一样,大小不一定一样。
(4)相似三角形定义本身揭示了相似三角形的性质:相似三角形对应角相等,对应边成比例。
(5)相似比带有顺序性,如 的相似比为
的相似比为

反过来 的相似比为
的相似比为
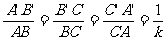
(6)全等三角形是相似比为1的相似三角形,但相似三角形不一定是全等三角形。
重点:掌握相似三角形的判定方法。
难点:灵活运用相似三角形的判定方法解决有关问题。
相似三角形的判定
5.已知函数: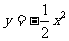 ,
, 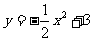 和
和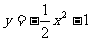 .
.
(1)分别画出它们的图象;
(2)说出各个图象的开口方向,对称轴和顶点坐标;
(3)说出函数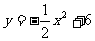 的图象的开口方向、对称轴和顶点坐标;
的图象的开口方向、对称轴和顶点坐标;
(4)试说明函数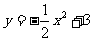 、
、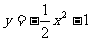 、
、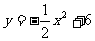 的图象分别有抛物线
的图象分别有抛物线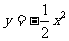 作怎样的平移才能得到?
作怎样的平移才能得到?
4.函数y=-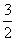 x
x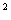 +3的图象,当x<0时,经过了第____象限;若图象上有两点(x
+3的图象,当x<0时,经过了第____象限;若图象上有两点(x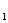 , y
, y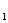 ),(x
),(x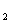 , y
, y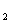 ),且满足x
),且满足x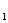 >x
>x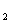 >0,则y
>0,则y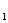 ____ y
____ y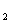 (填>,<或=);若只满足条件x
(填>,<或=);若只满足条件x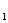 >x
>x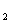 ,则能否判断y
,则能否判断y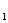 、y
、y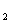 的大小关系?
的大小关系?
3.将抛物线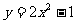 向上平移4个单位后,所得的抛物线是
,当x= 时,该抛物线有最 (填大或小)值,是
.
向上平移4个单位后,所得的抛物线是
,当x= 时,该抛物线有最 (填大或小)值,是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com