
本节课的两个例题均为补充的题目,其中例1是训练学生能正确去寻找相似三角形的对应边和对应角,让学生明确可类比全等三角形对应边、对应角的关系来寻找相似三角形中的对应元素:即(1)对顶角一定是对应角;(2)公共角一定是对应角;最大角或最小的角一定是对应角;(3)对应角所对的边一定是对应边;(4)对应边所对的角一定是对应角;对应边所夹的角一定是对应角.
例2是让学生会运用“三角形相似的预备定理”解决简单的问题,这里要注意,此题两次用到相似三角形的对应边成比例(也可以先写出三个比例式,然后拆成两个等式进行计算),学生刚开始可能不熟练,教学中要注意引导.
3.难点的突破方法
(1)要注意强调相似三角形定义的符号表示方法(判定与性质两方面),应注意两个相似三角形中,三边对应成比例, 每个比的前项是同一个三角形的三条边,而比的后项分别是另一个三角形的三条对应边,它们的位置不能写错;
每个比的前项是同一个三角形的三条边,而比的后项分别是另一个三角形的三条对应边,它们的位置不能写错;
(2)要注意相似三角形与全等三角形的区别和联系,弄清两者之间的关系.全等三角形是特殊的相似三角形,其特殊之处在于全等三角形的相似比为1.两者在定义、记法、性质上稍有不同,但两者在知识学习上有很多类似之处,在今后学习中要注意两者之间的对比和类比;
(3)要求在用符号表示相似三角形时,对应顶点的字母要写在对应的位置上,这样就会很快地找到相似三角形的对应角和对应边;
(4)相似比是带有顺序性和对应性的(这一点也可以在上一节课中提出):
如△ABC∽△A′B′C′的相似比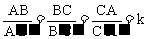 ,那么△A′B′C′∽△ABC的相似比就是
,那么△A′B′C′∽△ABC的相似比就是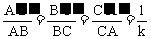 ,它们的关系是互为倒数.这一点在教学中科结合相似比“放大或缩小”的含义来让学生理解;
,它们的关系是互为倒数.这一点在教学中科结合相似比“放大或缩小”的含义来让学生理解;
(5)“平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似”定理也可以简单称为“三角形相似的预备定理”.这个定理揭示了有三角形一边的平行线,必构成相似三角形,因此在三角形相似的解题中,常作平行线构造三角形与已知三角形相似.
2.难点:三角形相似的预备定理的应用.
1.重点:相似三角形的定义与三角形相似的预备定理.
3.会运用“两个三角形相似的判定条件”和“三角形相似的预备定理”解决简单的问题.
2.掌握两个三角形相似的判定条件(三个角对应相等,三条边的比对应相等,则两个三角形相似)--相似三角形的定义,和三角形相似的预备定理(平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似).
1.经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步发展学生的探究、交流能力.
3. 让学生经历从实验探究到归纳证明的过程,发展学生的合情推理能力。
(教学重点与难点)
重点:判定两个三角形相似的预备定理
难点:探究两个三角形相似的预备定理的过程
(教学设计)
|
教学过程 |
设计意图说明 |
|
新课引入: 复习相似多边形的性质、定义及相似多边形相似比的定义 ↓ 相似三角形的定义、相似三角形相似比的定义及相似三角形的性质 ↓ 当k=1时,提出相似三角形与全等三角形的区别和联系 |
从相似多边形的概念以旧引新,帮助学生建立新旧知识间的联系,体会事物间一般到特殊﹑特殊到一般的关系。 强调相似与全等之间的一般与特殊的关系 |
|
提出问题: 如图27·2-1,在∆ABC中,点D是边AB的中点,DE∥BC, DE交AC于点E ,∆ADE与∆ABC有什么关系? 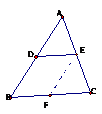 学生动手探究,小组合作,测量出两个三角形对应角、对应边的值,得到结论。 分析:观察27·2-1易知∠ADE=∠ABC,∠AED=∠ACB,∠A=∠A,即两三角形三组对应角分别相等,又知AD=  ,只需引导学生证得AE= ,只需引导学生证得AE=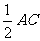 ,DE= ,DE=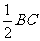 即可,即证明AE=EC。这样学生不难想到过E作EF∥AB。构造一个三角形与已知∆ADE全等。 即可,即证明AE=EC。这样学生不难想到过E作EF∥AB。构造一个三角形与已知∆ADE全等。↓ ∆ADE∽∆ABC,相似比为 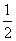 。 。延伸拓展问题: 改变点D在AB上的位置,先让学生猜想∆ADE与∆ABC仍相似,然后再用几何画板演示验证。 1.若D点为线段AB上任意一点, ∆ADE与∆ABC有什么关系? 2.若D点为AB延长线上任意一点, ∆ADE与∆ABC有什么关系? ↓ 归纳:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。  (A型)  (Z型) 几何语言: ∵ DE ∥ BC ∴ △ADE∽ △ABC |
让学生经历“猜想--探究--推理--证明”的过程,并通过特殊到一般的关系,最终归纳总结出结论。 突出结论的探索过程,重视实验操作度量和逻辑推理的有机结合。 通过观察特殊平行条件(经过三角形一边的中点平行于另一边)下两三角形的相似关系,引导学生思考一般平行条件(平行于三角形一边的直线和其他两边或者两边的延长线相交)下两三角形的相似关系,进一步体会事物间特殊到一般的关系。 通过几何画板演示,进一步验证猜想的结论,培养学生的实验探究意识。 用三种语言来描述,促进学生更深刻理解定理 给出两种典型的极具代表性的图形 |
巩固练习:
如图 已知如(图一)中DE∥BC,DF∥AC,(图二)中DE∥BC∥FG,请尽可能多地找出图中的相似三角形,并用符号表示。   ( 图一) ( 图一)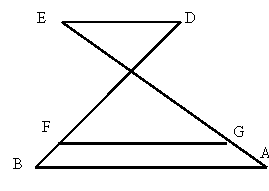  (图二) (图二) |
运用两个三角形相似判定的预备定理进行相关证明,让学生在练习中熟悉定理以及两三角形相似的表示法。 |
|
课堂小结:说说你在本节课的收获。 |
让学生及时回顾整理本节课所学的知识。帮助学生学会归纳,反思. |
|
布置作业: 1. 必做题: P55习题27·2题1 2. 选做题: P55习题27·2题4,5。 3. 备选题:如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形( ) A、1对 B、2对 C、3对 D、4对  |
分层次布置作业,让不同的学生在本节课中都有收获。 备选题答案:C |
2. 培养学生的观察﹑动手探究、归纳总结的能力,感受相似三角形与相似多边形;相似三角形与全等三角形的区别与联系,体验事物间特殊与一般的关系。
1. 了解相似比的定义,掌握判定两个三角形相似的方法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com