
2.(1)提出问题:首先,由三角形全等的SSS判定方法,我们会想如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么能否判定这两个三角形相似呢?
(2)带领学生画图探究;
(3)[归纳]
三角形相似的判定方法1 如果两个三角形的三组对应边的比相等, 那么这两个三角形相似.
1.复习提问:
(1) 两个三角形全等有哪些判定方法?
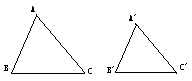 (2) 我们学习过哪些判定三角形相似的方法?
(2) 我们学习过哪些判定三角形相似的方法?
(3) 全等三角形与相似三角形有怎样的关系?
(4) 如图,如果要判定△ABC与△A’B’C’相似,是不是一定需要一一验证所有的对应角和对应边的关系?
本节课安排的两个例题,其中例1是教材P46的例1,此例题是为了巩固刚刚学习过的两种三角形相似的判定方法,(1)是复习巩固“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法;(2)是复习巩固“三组对应边的比相等的两个三角形相似” 的判定方法.通过此例题要让学生掌握如何正确的选择三角形相似的判定方法.
例2是补充的题目,它既运用了三角形相似的判定方法2,又运用了相似三角形的性质,有一点综合性,由于学生刚开始接触相似三角形的题目,而本节课的内容有较多,故此例题可以选讲.
3. 难点的突破方法
(1)关于三角形相似的判定方法1“三组对应边的比相等的两个三角形相似”,教科书虽然给出了证明,但不要求学生自己证明,通过教师引导、讲解证明,使学生了解证明的方法,并复习前面所学过的有关知识,加深对判定方法的理解.
(2)判定方法1的探究是让学生通过作图展开的,我们在教学过程中,要通过从作图方法的迁移过程,让学生进一步感受,由特殊的全等三角形到一般相似三角形,以及类比认识新事物的方法.
(3)讲判定方法1时,要扣住“对应”二字,一般最短边与最短边,最长边与最长边是对应边.
(4)判定方法2一定要注意区别“夹角相等” 的条件,如果对应相等的角不是两条边的夹角,这两个三角形不一定相似,课堂练习2就是通过让学生联想、类比全等三角形中SSA条件下三角形的不确定性,来达到加深理解判定方法2的条件的目的的.
(5)要让学生明确,两个判定方法说明:只要分别具备边或角的两个独立条件--“两边对应成比例,夹角相等”或“三边对应成比例”就能证明两个三角形相似.
(6)要让学生学会自觉总结如何正确的选择三角形相似的判定方法:这两种方法无论哪一个,首先必需要有两边对应成比例的条件,然后又有目标的去探求另一组条件,若能找到一组角相等,而这组对应角又是两组对应边的“夹角”时,则选用判定方法2,若不是“夹角”,则不能去判定两个三角形相似;若能找到第三边也成比例,则选用判定方法1.
(7)两对应边成比例中的比例式既可以写成如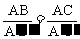 的形式,也可以写成
的形式,也可以写成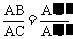 的形式.
的形式.
(8)由比例的基本性质,“两边对应成比例”的条件也可以由等积式提供.
2. 难点:(1)三角形相似的条件归纳、证明;
(2)会准确的运用两个三角形相似的条件来判定三角形是否相似.
1. 重点:掌握两种判定方法,会运用两种判定方法判定两个三角形相似.
3.能够运用三角形相似的条件解决简单的问题.
2.经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
1.初步掌握“三组对应边的比相等的两个三角形相似”的判定方法,以及“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法.
27.2.1 相似三角形的判定(二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com