1．经历两个三角形相似的探索过程，进一步发展学生的探究、交流能力．

27.2.1　 相似三角形的判定(三)

2．如图，AB•AC=AD•AE，且∠1=∠2，求证：△ABC∽△AED．

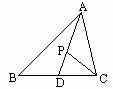
※3．已知：如图，P为△ABC中线AD上的一点，且BD²=PD•AD，

求证：△ADC∽△CDP．

教学反思

1．教材P47．1、3．

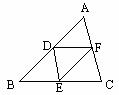
3．如图，△ABC中，点D、E、F分别是AB、BC、CA的中点，求证：△ABC∽△DEF．

2．如果在△ABC中∠B=30°，AB=5㎝，AC=4㎝，在△A’B’C’中，∠B’=30°A’B’=10㎝，A’C’=8㎝，这两个三角形一定相似吗？试着画一画、看一看？

1．教材P47．2．

例1(教材P46例1)

分析：判定两个三角形是否相似，可以根据已知条件，看是不是符合相似三角形的定义或三角形相似的判定方法，对于(1)由于是已知一对对应角相等及四条边长，因此看是否符合三角形相似的判定方法2“两组对应边的比相等且它们的夹角相等的两个三角形相似”，对于(2)给的几个条件全是边，因此看是否符合三角形相似的判定方法1“三组对应边的比相等的两个三角形相似”即可，其方法是通过计算成比例的线段得到对应边．

解：略

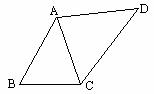※例2 (补充)已知：如图，在四边形ABCD中，∠B=∠ACD，AB=6，BC=4，AC=5，CD=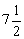，求AD的长．

分析：由已知一对对应角相等及四条边长，猜想应用“两组对应边的比相等且它们的夹角相等”来证明．计算得出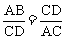，结合∠B=∠ACD，证明△ABC∽△DCA，再利用相似三角形的定义得出关于AD的比例式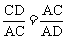，从而求出AD的长．

解：略(AD=)．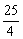

4．用上面同样的方法进一步探究三角形相似的条件：

(1)提出问题：由三角形全等的SAS判定方法，我们也会想如果一个三角形的两条边与另一个三角形的两条边对应成比例，那么能否判定这两个三角形相似呢？

(2)让学生画图，自主展开探究活动．

(3)[归纳]

三角形相似的判定方法2　 两个三角形的两组对应边的比相等，且它们的夹角相等，那么这两个三角形相似．

3．(1)提出问题：怎样证明这个命题是正确的呢？

(2)教师带领学生探求证明方法．