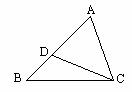
2．已知：如图，∠1=∠2=∠3，求证：△ABC∽△ADE．

1．教材P49的练习1、2．

　　 例1(教材P48例2)．

分析：要证PA•PB=PC•PD，需要证，则需要证明这四条线段所在的两个三角形相似．由于所给的条件是圆中的两条相交弦，故需要先作辅助线构造三角形，然后利用圆的性质“同弧上的圆周角相等”得到两组角对应相等，再由三角形相似的判定方法3，可得两三角形相似．

证明：略(见教材P48例2)．

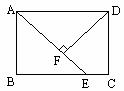
例2 (补充)已知：如图，矩形ABCD中，E为BC上一点，DF⊥AE于F，若AB=4，AD=5，AE=6，求DF的长．

分析：要求的是线段DF的长，观察图形，我们发现AB、AD、AE和DF这四条线段分别在△ABE和△AFD中，因此只要证明这两个三角形相似，再由相似三角形的性质可以得到这四条线段对应成比例，从而求得DF的长．由于这两个三角形都是直角三角形，故有一对直角相等，再找出另一对角对应相等，即可用“两角对应相等，两个三角形相似”的判定方法来证明这两个三角形相似．

解：略(DF=)．

1．复习提问：

(1)我们已学习过哪些判定三角形相似的方法？

(2)如图，△ABC中，点D在AB上，如果AC²=AD•AB，

那么△ACD与△ABC相似吗？说说你的理由．

(3)如(2)题图，△ABC中，点D在AB上，如果∠ACD=∠B，

那么△ACD与△ABC相似吗？--引出课题．

(4)教材P48的探究3 ．

本节课安排了两个例题，例1是教材P48的例2，是一个圆中证相似的题目，这个题目比较简单，可以让学生来分析、让学生说出思维的方法、让学生自己写出证明过程．并让学生掌握遇到等积式，应先将其化为比例式的方法．

例2是一个补充的题目，选择这个题目是希望学生通过这个题的学习，掌握利用三角形相似的知识来求线段长的方法，为下节课学习“27.2.2 相似三角形的应用举例”打基础．

3．难点的突破方法

(1)在两个三角形中，只要满足两个对应角相等，那么这两个三角形相似，这是三角形相似中最常用的一个判定方法．

(2)公共角、对顶角、同角的余角(或补角)、同弧上的圆周角都是相等的，是判别两个三角形相似的重要依据．

(3)如果两个三角形是直角三角形， 则只要再找到一对锐角相等即可说明这两个三角形相似．

2．难点：三角形相似的判定方法3的运用．

1．重点：三角形相似的判定方法3--“两角对应相等，两个三角形相似”

3．能够运用三角形相似的条件解决简单的问题．

2．掌握“两角对应相等，两个三角形相似”的判定方法．