7．平面直角坐标系中，有一条鱼，它有六个顶点，下列说法中正确的是(　)

A．将各点横坐标乘以2，纵坐标不变，得到的鱼与原来的鱼位似．

B．将各点纵坐标乘以2, 横坐标不变，得到的鱼与原来的鱼位似．

C．将各点横、纵坐标都乘以2，得到的鱼与原来的鱼位似．

D．将各点横坐标乘以2，纵坐标乘以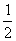，得到的鱼与原来的鱼位似．

[考点分析]考查以原点为位似中心，两位似图形坐标之间的关系．

[名师点评]

平面直角坐标系中，以原点为位似中心，两位似图形横、纵坐标之比都为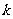或－．

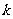[正确答案]C

6．在如图所示的四个图案中的两个图形可以看作是位似变换得到的是(　)．

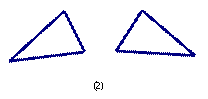
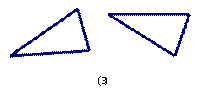
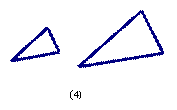
A．(1)(2)　 B．(1)(3)　 C．(3)(4)　　 D．(1)(4)

[考点分析]考查位似图形的判断．

[名师点评]

位似图形的判断要根据定义，须符合三个条件：①相似，②对应边平行或在同一直线上，③对应顶点的连线交与一点．

[正确答案]D

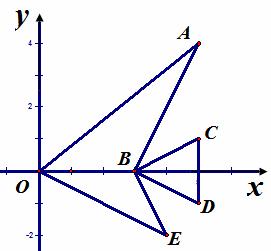
5．△OCD与△OAB是位似图形，其中位似比为2∶3，若将两个图形放大，使放大前后对应线段的比为1∶2，则放大后两个三角形的位似比为(　　)．

A．4∶3　B．1∶3　C．2∶3　D．1∶2

[考点分析]考查位似比与相似比的关系．

[名师点评]

位似比即位似图形的相似比，亦为对应点到位似中心的距离比，相似比为相似图形对应边的比，△OCD与△OAB都放大2倍后相似比不变．

[正确答案]C

4．用作位似形的方法，可以将一个图形放大或缩小，位似中心(　　)

A．只能选在原图形的外部．

B．只能选在原图形的内部．

C．只能选在原图形的边上．

D．可以选择任意位置．

[考点分析]考查位似中心的概念．

[名师点评]位似图形的位似中心可以选择平面内的任意位置．

[正确答案]D

3．若两个图形位似，则下列叙述不正确的是(　　)

A．每对对应点所在的直线相交于同一点．

B．两个图形上的对应线段之比等于位似比．

C．两个图形上的对应线段必平行．

D．两个图形的面积之比等于位似比的平方．

[考点分析]考查两个位似图形之间的关系．

[名师点评]

由位似图形的定义可知，两个图形位似必须符合三个条件：①相似，②对应边平行或在同一直线上，③对应顶点的连线交与一点．对应线段有可能在同一直线上，所以选项C错误．

[正确答案]C

2．下列判断中，正确的是(　)

A．相似图形一定是位似图形．　

B．位似图形一定是相似图形．

C．全等的图形一定是位似图形．

D．位似图形一定是全等图形．

[考点分析]考查相似图形、位似图形、全等图形之间的关系．

[名师点评]

位似图形是相似图形的一种特殊情况，所以位似图形肯定是相似图形，而相似图形不一定是位似图形；全等又是相似的特殊情况，与位似没有直接联系，全等的图形不一定是位似图形，位似图形也不一定是全等图形．

[正确答案] B

1．位似图形上某一对对应点到位似中心的距离分别是10cm和5cm，则他们的位似比是___________．

[考点分析]考查位似比的概念．

[名师点评]位似比即位似图形的相似比，亦为对应点到位似中心的距离比．

[正确答案]2　

2．已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．(1)求证：AC•BC=BE•CD；

　 (2)若CD=6，AD=3，BD=8，求⊙O的直径BE的长．

教学反思

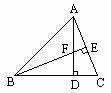
1．　　 已知：如图，△ABC 的高AD、BE交于点F．

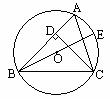求证：．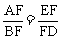

3．下列说法是否正确，并说明理由．

(1)有一个锐角相等的两直角三角形是相似三角形；

(2)有一个角相等的两等腰三角形是相似三角形．