
1.根据实际问题中给定的函数关系式,结合图形来分析其中的数量关系,找出解决问题的方法;
问题1 解答
(1)由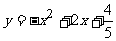 得
得 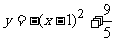 ,所以其顶点坐标是(1,
,所以其顶点坐标是(1,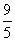 ),所以喷出的水流距水平面的最大高度是
),所以喷出的水流距水平面的最大高度是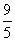 m.
m.
(2) B点的坐标是抛物线与x轴的交点,由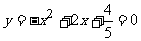 可解得(
可解得(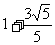 ,0)或(
,0)或(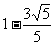 ,0),取(
,0),取(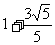 ,0),它和点O的距离是(
,0),它和点O的距离是(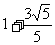 )m,所以当水池的半径只要大于(
)m,所以当水池的半径只要大于(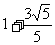 )m时,喷出的水流都落在水池内.
)m时,喷出的水流都落在水池内.
问题2 解答
设洞口截面所成抛物线的函数关系式为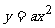 ( a<0 ) (1).
( a<0 ) (1).
因为当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m,所以点B的坐标为(0.8,-2.4),因为点B在抛物线上,将它的坐标代入(1),得
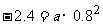 ,
,
所以 a=-3.75.
因此,函数关系式是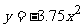 (2).
(2).
因为FC=1.5m,所以OF=OC-FC=2.4-1.5=0.9(m),根据(2)可得
-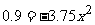
解得x=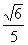 或x=-
或x=-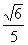 ,所以D点的坐标是(
,所以D点的坐标是(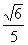 ,-0.9),所以ED=
,-0.9),所以ED=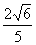 <1,所以,当离开水面1.5m处,涵洞宽ED是
<1,所以,当离开水面1.5m处,涵洞宽ED是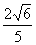 m,不会超过1m.
m,不会超过1m.
问题1
某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高为0.8m.水流各个方向上沿形状相同的抛物线路径落下,如图(1)所示.
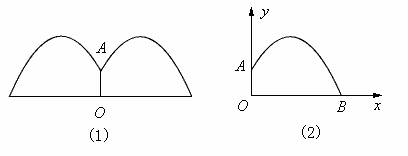
根据设计图纸已知:在图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是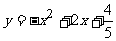 .
.
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
在学生有困难的时候可作如下帮助
分析 (1)从图象上可观察到,喷出的水流距水平面的最大高度就是抛物线的顶点的纵坐标,所以只要求出其顶点坐标就可以了.
(2) 从图象上可观察到,水池的半径只要大于点O与抛物线和x轴的交点B点的距离,喷出的水流都落在水池内.
问题2
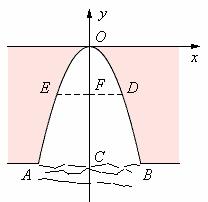
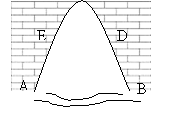
一个涵洞成抛物线形,它的截面如图.现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m.这时,离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
在学生有困难的时候可作如下帮助
分析 根据已知条件,要求ED宽,只要求出FD的长度.在图示的直角坐标系中,即只要求出点D的横坐标.
因为点D在涵洞所成的抛物线上,又由已知条件可得到点D的纵坐标,所以利用抛物线的函数关系式可以进一步算出点D的横坐标.你会求吗?
生活中,我们常会遇到与二次函数及其图象有关的问题,例如公园的喷水池,喷出的水柱形状有的就是抛物线形,请与同伴共同研究,尝试解决下面的问题.
2. 学情分析:
学生已经学习过了二次函数的图像及其性质,同时已有用数学知识解决实际问题的经验。而我所任教班级的学生个性活泼,思维活跃但欠缺严谨;学生学习基础较好,初步具有对数学问题进行合作探究的意识与能力。
拓
展
转
化,
加
深
理
解

§27.3 二次函数的实践与探索 课堂卷
例1:某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水。连喷头在内,柱高为0.8m。水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示
1)喷出的水流距水平面的最大高度是多少?
 2) 如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
2) 如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
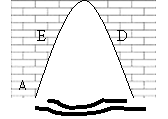
例2:一个涵洞的截面边缘成抛物线形,如图,当水面宽AB=1.6m时,测得涵洞顶点与水面的距离为2.4m,
1)建立适当的平面直角坐标系,求出抛物线的函数解析式;
2)离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
3)一只宽为1m,高为1.5m的小船能否通过?为什么?
教案说明:
1.教材的地位和作用:
本课内容是华东师大版数学九年级下册第27章第3节。按照华东师大版教材的安排,在八年级讲授一次函数与反比例函数,在九年级把二次函数独立成章,专门讲授二次函数的图像及性质,并在本章的最后安排了这一节《二次函数的实践与探索》。
“实践与探索”作为新课程的一个有机成分,在“数与代数”板块中屡见不鲜,其设计意图是:让学生投入解决问题的实践活动,经历数学建模的全过程,初步领会数学建模的思想和方法,提高数学的应用意识和解决实际问题的能力。事实上,根据社会发展的需要,数学建模成为了中学数学的一条主线,这种思想的建立无论是对学生的后继学习还是对其终身需求都有着直接的影响。
本节“实践与探索”从体现生活中的抛物线的两个典型模型(喷水池和涵洞)入手,探索了现实物状与二次函数模型的对应关系,教会学生使用数学工具并用来合理解释数学模型。而后安排了用图像法解一元二次不等式及不等式组,安排用时4个课时,我今天说课选取的是第一课时--典型二次函数模型。
4.行驶中的汽车在刹车后由于惯性的作用,还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能﹙车速不超过140千米/时﹚,对这种汽车进行测试,数据如下表:
|
刹车时车速(千米/时) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
刹车距离 |
0 |
0.3 |
1.0 |
2.1 |
3.6 |
5.5 |
7.8 |
﹙1﹚以车速为x轴,以刹车距离为y轴,在坐标系中描出这些数据所表示的点,并用平滑的曲线连结这些点,得到函数的大致图象;
﹙2﹚观察图象,估计函数的类型,并确定一个满足这些数据的函数关系式;
﹙3﹚该型号汽车在国道上发生一次交通事故,现场测得刹车距离为46.5米,请推测刹车时的车速是多少?请问在事故发生时,汽车是超速行驶还是正常行驶?
[本课学习体会]
3.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式;
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
B组
2.某旅社有客房120间,当每间房的日租金为50元时,每天都客满,旅社装修后,要提高租金,经市场调查,如果一间客房日租金增加5元,则客房每天出租数会减少6间,不考虑其他因素,旅社将每间客房日租金提高到多少元时,客房的总收入最大?比装修前客房日租金总收入增加多少元?
1.某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),
与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204。
(1)写出商场卖这种服装每天的销售利润y与每件的销售价x之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com