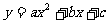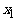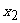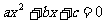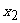1.二次函数与一元二次方程的关系：二次函数与x轴的两个交点的横坐标、是一元二次方程的两根、；反之也成立；由可判断二次函数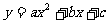与x轴的交点的情况；

例1 抛物线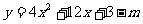与x轴只有一个交点，试求m的值？

解 因为 抛物线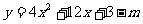与x轴只有一个交点，

所以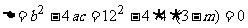 　

由此解得 m＝-6.

注　本题可变形为：“抛物线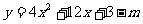的顶点在x轴上，试求m的值？”

解答相同.

例2 抛物线与x轴有两个不同的交点，试求m的取值范围？

解 因为 抛物线与x轴有两个不同的交点，

所以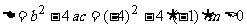 　

由此解得 m ＞ -4.

例3 已知二次函数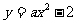的图象过点(1，-1)，求这个二次函数的解析式，并判断函数的图象与x轴的交点的个数.

解 因为 二次函数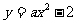的图象过点(1，-1)，

所以 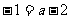，即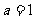

所以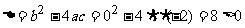 　

所以 这个二次函数的解析式是，函数的图象与x轴的有两个交点.

思考

(1)如何求方程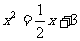的解

(2)你能求不等式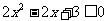的解吗？

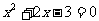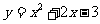2.(1)一元二次方程的解为　　　　　　 ；那么二次函数与x轴的交点坐标为　　　　　　 ；　　　　　　　 .

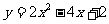(2)一元二次方程的解为　　　　　　 ；那么二次函数与x轴的交点坐标为　　　 　　　；　　　　　　　 .

(3)一元二次方程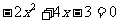的解的情况　　　　　　 ；那么二次函数与x轴的交点的情况为　　　　　　　　　　 .

归纳 二次函数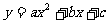与x轴的两个交点的个数有三种情况：两个、一个、没有.

由学生练习 2的(1)、(2)、(3)可知：二次函数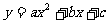与x轴的交点的个数与一元二次方程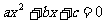的根的情况有关，即与根的判别式有关.

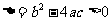当，二次函数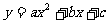与x轴有两个不同的交点；

当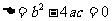，二次函数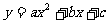与x轴有一个交点；

当，二次函数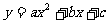与x轴没有交点；

反之也成立.

学生练习 任取一个二次函数，判断它与x轴的交点的个数.

试一试

根据问题3的图象回答下列问题.

(1)当x取何值时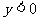，；当x取何值时，？

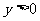(2)能否用含有x的不等式来描述(1)中的问题？

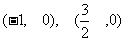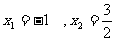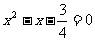　　图象与x轴的两个交点的坐标为，交点的横坐标为.方程的两个根为.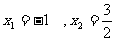

　 　归纳 二次函数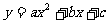与x轴的两个交点的横坐标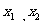是一元二次方程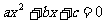的两根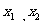；反之也成立.

学生练习 填空

1.二次函数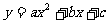与x轴的两个交点坐标为(-1,0)、(5,0)，则一元二次方程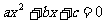的两根为　　　　　 .

问题 画出函数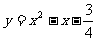的图象，根据图象回答下列问题.

(1)图象与x轴的交点坐标是什么？

(2)当x取何值时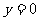，？这里的x的取值与方程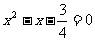有什么关系？

(3)你能从中得到什么启发？

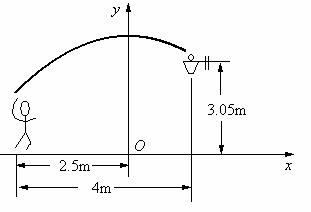
4.如图，一位篮球运动员在离篮球水平距离4 m处跳起投篮，球沿一条抛物线运行，当球运行的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内.已知篮圈中心离地面的距离为3.05m.

(1)建立如图所示的直角坐标系，求抛物线所对应的函数关系式；

(2)若该运动员身高1.8m，这次跳投时，球在他头顶上方0.25m处出手.问：球出手时，他跳离地面多高？

3.某商人开始时，将进价为每件8元的某种商品按每件10元出售，每天可销出100件.他想采用提高售价的办法来增加利润.经试验，发现这种商品每件每提价1元，每天的销售量就会减少10件.

(1)写出售价x(元/件)与每天所得的利润y(元)之间的函数关系式；

(2)每件售价定为多少元，才能使一天的利润最大？

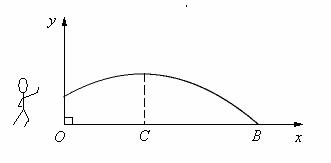
2.如图，一个运动员推铅球，铅球在点A处出手，出手时球离地面约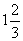m；铅球落地在点B处. 铅球运行中在运动员前4m处(即OC＝4)达到最高点，最高点高为3m．已知铅球经过的路线是抛物线，根据图示的直角坐标系，你能算出该运动员的成绩吗？

1.某公园要建造圆形的喷水池，在水池中央垂直于水面处安装一个柱子OA(如图(1))，O恰在水面中心，OA＝1.25米.由柱子顶端A处的喷水头向外喷水，水流向各个方向沿形状相同的抛物线落下.为使水流形状较为漂亮，要求设计成水流在离OA距离为1米处达到距水平最大高度2.25米.

　(1)如果不计其他因素，那么水池的半径至少要多少米，才能使喷出的水流不致落到池外?

　(2)若水流喷出的抛物线形状与(1)相同，水池的半径为3.5米，要使水流不落到池外，此时水流最大高度应达多少米(精确到0.1米)?

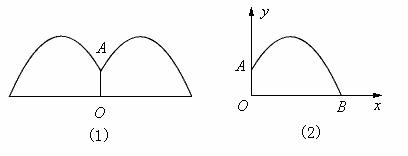
(提示：建立如图(2)所示的直角坐标系.)

2.有时要根据实际问题，再结合图形，先求出图形的函数关系式，再利用函数的图象的知识来解决问题．