11.如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA²+OB²= 17, 且线段OA、OB的长度是关于x的一元二次方程x²-mx+2(m-3)=0的两个根.

　　 (1)求C点的坐标;

　　 (2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.

　　 (3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.

(三)多变题(8分)

10.如图所示,在直角坐标系xOy中,A,B是x轴上两点,以AB为直径的圆交y轴于点C,设过A、B、C三点的抛物线关系为y=x²-mx+n,若方程x²-mx+n=0两根倒数和为-2.

　　 (1)求n的值;

(2)求此抛物线的关系式.

(二)多解题(8分)

9.已知抛物线y=2x²-kx-1与x轴两交点的横坐标,一个大于2,另一个小于2,试求k的取值范围.

(一)教材中的变型题(14分)

8.(教材P22问题3变型)画出函数y=x²-x- 的图象,根据图象回答问题:

　 (1)图象与x轴交点A的坐标_________,B点的坐标________,与y轴交点C 的坐标________,=________.(A点在B点左边).

　 (2)该函数的对称轴方程为_______,顶点P的坐标________,=______.

　 (3)当______时,y≤0;当x_______时,y≥0.

　 (4)抛物线开口向________,函数y有最_____值;当x=_____时,y最值=______.

7.某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=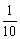x²+5x+1000,Q=-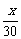+45.

　 (1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;

　 (2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?

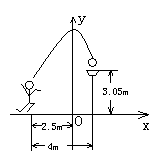
6.如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.

　 (1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;

　 (2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?

5.利用函数图象求方程组 的解.

4.利用函数图象求2x²-x-3=0的解.

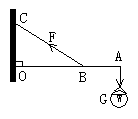
3.如图所示,长为1.2m的轻质杆OA可绕竖直墙上的O点自由转动,A端挂有G=8N的吊灯.现用长为0.8m的细绳,一端固定在墙上C点,另一端固定在杆上B点,而使杆在水平位置平衡.试求OB为多长时绳对杆的拉力最小,最小拉力为多少?

2.已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=.

　 (1)求这条抛物线的关系式.

　 (2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.