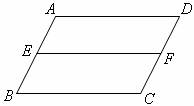
3.如图，已知四边形ABCD是平行四边形，点E、F分别是边AB、DC的中点．求证：EF＝BC．

2.求证：平行四边形的对角线互相平分．

1.求证：两组对边分别相等的四边形是平行四边形．

3.可以用有关平行四边形知识证明的问题，不要倒退到利用三角行的全等来证明．

2.在证明有关平行四边形问题时，要根据已知条件的特征，正确合理地使用平行四边形的性质与判定；

例1 如图，在平行四边形ABCD中，E、F分别是边AB、CD上的点，且AE＝CF．

求证：BF∥DE．

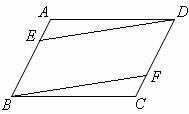
分析 要证BF∥DE，只要证四边形EBFD是平行四边形即可

证明 因为四边形ABCD是平行四边形，

所以AB∥CD，AB＝CD．

因为AE＝CF，

所以BE＝DF．

又因为BE∥DF，

所以四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)．

所以BF∥DE．

变式应用：如图，在平行四边形ABCD中，E、F分别是对角线AC上的两点，且AE＝CF，那么 BF∥DE成立吗？

学生通过充分的交流后，一致得出：连结BD交AC于O点，利用“对角线互相平分的四边形是平行四边形”来证明最为合适．

知识回顾：要证明一个命题须分三步来完成：①画图；②结合图形写出已知、求证；③证明．

已知：如图所示，在四边形ABCD中，AB∥CD，AB＝CD．

求证：四边形ABCD是平行四边形．

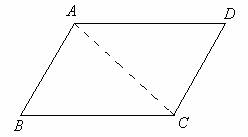
分析 要证明四边行ABCD是平行四边形，目前只能用平行四边形的定义来证明，即只要证明另一组对边平行即可，因此可以连结其中一条对角线，利用全等三角形对应角相等来证明内错角相等．

证明 连结AC．因为四边形ABCD是平行四边形，

所以AB∥CD，

所以∠BAC＝∠DCA(两直线平行，内错角相等)．

在△ABC和△CDA中，因为AB＝CD，∠BAC＝∠DCA，AC＝CA，

所以△ABC≌△CDA(S.A.S)，

所以∠BCA＝∠DAC，

所以BC∥DC，

所以四边形ABCD是平行四边形．

于是得：

平行四边形判定定理1　一组对边平行且相等的四边形是平行四边．

利用全等三角形的性质，同样可以证明下列平行四边形判定定理．

平行四边形判定定理2　两组对边分别相等的四边形是平行四边形．

平行四边形判定定理3　两组对角分别相等的四边形是平行四边形．

平行四边形判定定理4　对角线互相平分的四边形是平行四边形．

同样，我们也可用逻辑推理的方法来证明平行四边形的性质．

平行四边形性质定理1　平行四边形的对边相等．

已知： 如图，四边形ABCD是平行四边形．

求证： AB＝CD， BC＝DA．

分析 要证明平行四边形的对边相等，可以连结其中一条对角线，把平行四边形分成两个三角形，然后利用全等三角形对应边．相等得

证明 连结AC．因为四边形ABCD是平行四边形，

所以AB∥CD，

　　 所以∠BAC＝∠DCA(两直线平行，内错角相等)．

同理∠BCA＝∠DAC．

在△ABC和△CDA中，因为∠BAC＝∠DCA，AC＝CA，∠BCA＝∠DAC，

所以△ABC≌△CDA(A.S.A.)，

所以AB＝CD，BC＝DA(全等三角形的对应边相等)．

由△ABC≌△CDA，我们还可以得出∠B＝∠D，同样也可得出∠BAD＝∠DCB，于是可得：

平行四边形性质定理2　平行四边形的对角相等．

同样，我们也可证明：

平行四边形性质定理3　平行四边形的对角线互相平分．

在第12章中，我们已学过平行四边形的性质与判定，你能用逻辑推理的方法来证明“一组对边平行且相等的四边形是平行四边形”吗？

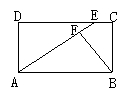
20.(2003,北京朝阳,7分)已知:如图所示,在矩形ABCD中,E为DC上的一点,BF ⊥AE于点F,且BF=BC,求证:AE=AB.