例1 如图，在菱形ABCD中，M是AB的中点，且DM⊥AB，则ΔABD是什么三角形?

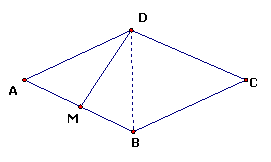
解 连结BD．

因为四边形ABCD是菱形，

所以AD＝AB．

又因为DM⊥AB, M是AB的中点，

所以DM垂直平分AB．

所以AD＝BD，

所以AD＝BD＝AB．

所以ΔABD是等边三角形．

例2 如图，AD是ΔABC的角平分线，DE∥AC交AB于E，DE∥BA交AC于F．猜想AD与EF是什么关系?

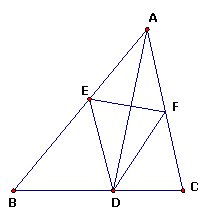
解 因为DE∥BA，DE∥AC．

所以四边形AEFD为平行四边形，

又因为AD是ΔABC的角平分线，

所以∠EAD＝∠FAD．

因为DE∥AC，

所以∠FAD＝∠ADE．

所以∠EAD＝∠ADE．

所以ED＝EA．

所以平行四边形AEFD为菱形．

所以AD⊥EF，且AD与EF相互平分．

我们知道菱形是特殊的平行四边形，因此它具有平行四边形的性质，而且还具有一些特殊的性质．

根据菱形的定义，菱形是平行四边形，且有一组邻边相等，从而可得：

定理菱形的四条边都相等．

由问题(2)我们还知道

定理　菱形的对角线互相垂直，并且每一条对角线平分一组对角．

会用推理的方法证明吗？

已知：如图，四边形ABCD是菱形．

求证：AC⊥BD；AC平分∠DAB，CA平分∠BCD，BD平分∠ABC，DB平分∠CDA．

分析 要证AC⊥BD，AC平分∠DAB，只要证明△DAB是等腰三角形，且AC平分BD．

证明 设对角线AC与BD交于点O．

因为四边形ABCD是菱形，故AB＝AD，

即△ABD为等腰三角形．

又BO＝DO(平行四边形的对角线互相平分)，所以AC⊥BD，AC平分∠DAB(等腰三角形的三线合一)．

同理，CA平分∠BCD，BD平分∠ABC，DB平分∠CDA．

要判定一个四边形是不是菱形，除了利用菱形的定义直接判定外，还有如下的判定定理：

定理　四条边相等的四边形是菱形

思考　根据对角线之间的关系能否判定一个平行四边形是菱形呢？

再看上面一个活动的平行四边形木框,保持内角大小不变，仅改变边的大小，观察对角线的变化，当对角线具有什么性质时，平行四边形变为菱形？

定理　对角线互相垂直的平行四边形是菱形

教师出示教具：“一个活动的平行四边形木框”，用两根橡皮筋分别套在相邻的两个顶点上．平行移动另一对相邻的顶点B、C，立即改变平行四边形的形状．

学生思考如下问题：

(1)无论BC平行移到什么位置，四边形ABCD还是平行四边形吗？

(2)当BC移动什么位置时，这个平行四边形就变成一个特殊的平行四边形--菱形？这时两条对角线有什么位置关系？

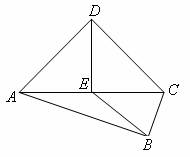
2.如图，已知∠ABC＝∠ADC＝90°，点E是AC的中点．

求证：EB＝ED．

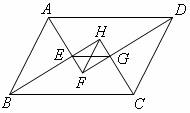
1.已知：平行四边形ABCD的四个内角的平分线交于E、F、G、H．

求证：EG＝HF．

2.矩形的判定：

(1)有三个角是直角的四边形是矩形；

(2)有一个内角是直角的平行四边形是矩形；

(3)两条对角线相等的平行四边形是矩形．

1.矩形的性质：

(1)矩形具有平行四边形的一切性质；

(2)矩形的四个内角都是直角；

(3)矩形的对角线相等且互相平分．

例1 求证：直角三角形斜边上的中线等于斜边的一半．

已知：如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线．

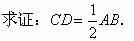
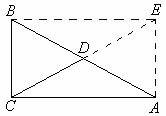
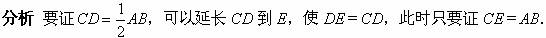
本题的关键在于证明四边形AEBC是一个矩形．

证明　延长CD到E，使DE＝CD，连结BE、AE．

因为CD是斜边AB上的中线，

所以AD＝BD．

又因为CD＝DE，

所以四边形BCAE为平行四边形．

又因为∠ACB＝90°，

所以平行四边形BCAE为矩行．

所以CE＝AB．

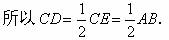
即直角三角形斜边上的中线等于斜边的一半．

以后把这条作为直角三角行的性质定理．

我们知道矩形是特殊的平行四边形，因此它具有平行四边形的性质，而且还具有一些特殊的性质．

根据矩形的定义，矩形是平行四边形，且有一个角是直角，从而可得：

定理矩形的四个角都是直角．

由问题(3)我们还知道定理“矩形的对角线相等”．你会用推理的方法证明吗？

已知：如图，四边形ABCD是矩形．

求证：AC＝BD．

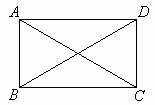
分析 由于AC、BD分别是△ABC、△DCB的边，因此要证AC＝BD，只要证△ABC≌△DCB．

证明 因为四边形ABCD是矩形．

所以AB＝CD，∠ABC＝∠DCB．

又因为BC＝BC，

所以ΔABC≌ΔDCB(S.A.S)．

所以AC＝BD．

上述两条定理是矩行的性质定理．

那么要判定一个四边形是不是矩形，除了利用矩形的定义直接判定外，还有如下的判定定理：

定理　有三个角是直角的四边形是矩形．

思考　根据对角线之间的关系能否判定一个平行四边形是矩形呢？

再看上面一个活动的平行四边形木框,保持边的大小不变，仅改变内角大小，观察对角线的变化，当对角线具有什么性质时，平行四边形变为矩形．

定理　对角线相等的平行四边形是矩形．

上述两条定理是矩行的判定定理

教师出示教具：“一个活动的平行四边形木框”，用两根橡皮筋分别套在相对的两个顶点上．拉动一对不相邻的顶点A、C，立即改变平行四边形的形状．

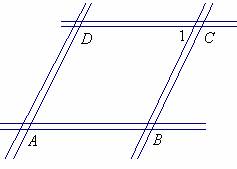
学生思考如下问题：

(1)无论∠1如何变化，四边形ABCD还是平行四边形吗？

(2)随着∠1的变化，两条对角线长度有没有变化？

(3)当∠1为什么角时，这个平行四边形就变成一个特殊的平行四边形--矩形？这时两条对角线长度有没有关系？