2.正方形具有矩形的一切性质：四个角都是直角，对角线相等；

1.正方形具有平行四边形的一切性质：两组对边平行且相等，两组对角相等，对角线互相平分；

例1　求证：依次连结正方形各边中点所成的四边形是正方形．

已知：如图27.3.7，在正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA的中点．

求证：四边形EFGH是正方形．

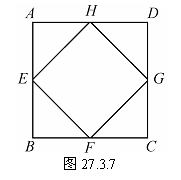
分析　要证四边形EFGH是正方形，可先证四边形EFGH是矩形，然后再证有一组邻边相等；也可先证四边形EFGH是菱形，然后再证有一个角是直角．

证明　因为四边形ABCD是正方形，所以∠B＝∠C＝90°，AB＝BC＝CD．

因为点E、F、G分别是AB、BC、CD的中点，

所以BE＝BF＝CF＝CG，

∠BEF＝∠BFE＝∠CFG＝∠CGF＝45°，

因此∠EFG＝90°．

同理FGH＝∠GHE＝90°．

所以四边形EFGH是矩形(有三个角是直角的四边形是矩形)．

因为BE＝CF，∠B＝∠C，BF＝CG，

所以△BEF≌△CFG(S.A.S.)，

EF＝FG(全等三角形的对应边相等)．

所以四边形EFGH是正方形(有一组邻边相等的矩形是正方形)

提问：你能用分析中的第二种方法证明吗？

变式应用　如图，已知点A′B′C′D′分别是正方形ABCD四条边上的点，并且AA′＝BB′＝CC′＝DD′，求证：四边形A′B′C′D′是正方形．

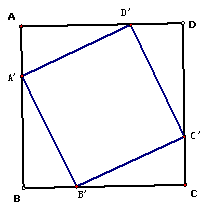
分析　 证明方法类同上例，请同学们自己完成．

我们已经知道正方形既是矩形，又是菱形，因此，正方形具有矩形和菱形的所有性质．

定理　正方形的四个角都是直角，四条边都相等．正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角．

反之，如果一个四边形既是矩形，又是菱形，那么这个四边形一定是正方形．于是可得：

定理　有一个角是直角的菱形是正方形．

定理有一组邻边相等的矩形是正方形．

2.展开一边固定对边活动的矩形．

将活动的矩形架的CD边左右移动时，问：图中CD在移动时，这个图形始终是怎样的图形？(CD在活动的过程中始终保持与AB平行)生答：矩形．当CD移动到C′D′位置，且AC′＝AB时，此时的图形还是矩形吗？这时生回答：是，是矩形，但它是特殊的矩形，也是正方形．

1.展开活动的衣帽架(如图)．

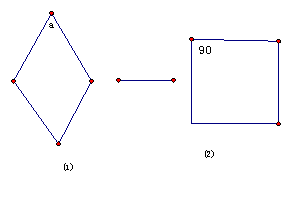
图(1)的α在不断的地变化过程中．这个图形始终是怎样的图形？生答：菱形．老师继续问当α＝90°时，这个图形还是菱形吗？如上图(2)．有的生答：不是，是正方形．有的生答：是，还是菱形，是一个特殊的菱形．最后老师进行评判，并指出：当α＝90°时，这个四边形还是菱形．因为它是邻边相等的平行四边形．但它是特殊的菱形是一个内角为直角的菱形也是正方形．

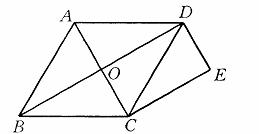
2.如图，O是菱形ABCD的对角线的交点，DE∥AC，CE∥BD．求证：四边形OCED是矩形．

1.有一条对角线平分一个内角的平行四边形是否是菱形？如果是，请给出证明；如果不是，请举出反例．

2.菱形的判定：

(1)四条边相等的四边形是菱形；

(2)有一组邻边相等平行四边形是菱形；

(3)对角线互相垂直的平行四边形是菱形．

1.菱形的性质：

(1)菱形具有平行四边形的一切性质；

(2)菱形的四条边都相等；

(3)菱形的对角线互相垂直，并且每一条对角线平分一组对角．