2.等腰梯形的判定：

(1)由定义得两腰相等的梯形是等腰梯形；

(2)同一底上两个内角相等的梯形是等腰梯形；

(3)两条对角线相等的梯形是等腰梯形．

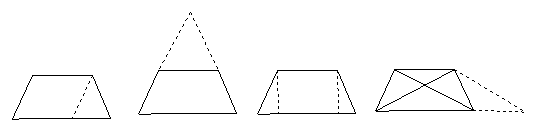
(4)常见的添线方法：

1.等腰梯形的性质：

(1)由定义得等腰梯形的两腰相等；

(2)等腰梯形是轴对称图形；

(3)等腰梯形的两条对角线相等；

(4)等腰梯形同一底上两个内角相等．

例1　用图中所示的辅助线的方法，证明同一条底边上的两个内角相等的梯形是等腰梯形．

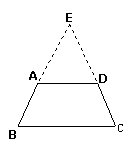
已知：如图27.3.10，在梯形ABCD中，AD∥BC，∠B＝∠C．

求证：四边形ABCD是等腰梯形．

证明　延长BA和CD交于E．

因为∠B＝∠C，

所以BA＝CE．

有因为AD∥BC，

所以∠B＝∠EAD，∠C＝∠EDA，

所以∠EAD＝∠EDA．

所以AE＝DE．

所以BE-BA＝CE-CD，

即AB＝CD，

所以四边形ABCD是等腰梯形．

例2　如图，在等腰梯形ABCD中，AB∥DC，AD＝BC，且AC⊥BD，CH是高．

求证：AB+CD＝2CH．

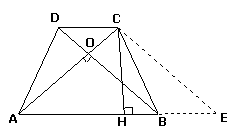
证明　过C作CE∥DB，交AB的延长线于E．

因为AB∥DC，CE∥DB，

所以四边形DBEC是平行四边形．

所以CD＝BE，CE＝BD．

又因为等腰梯形ABCD，

所以AC＝BD，

所以AC＝CE．

又因为CH是高，

所以AH＝HE．

因为AC⊥BD，CE∥DB，

所以AC⊥CE．

所以2CH＝AE＝AB+BE＝AB+DC，

即AB+DC＝2CH．

定理　等腰梯形的同一条底边上的两个内角相等．

已知：如图27.3.8，在梯形ABCD中，AD∥BC，AB＝DC．

求证：∠ABC＝∠DCB，∠BAD＝∠CDA．

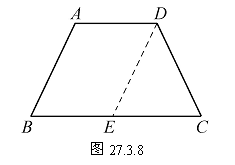
分析　可以过点D作DE∥AB，交BC于E．

(请学生写出完整的证明过程)

定理　等腰梯形的两条对角线相等．

已知：如图27.3.9，在梯形ABCD中，AD∥BC，AB＝DC．

求证：AC＝BD．

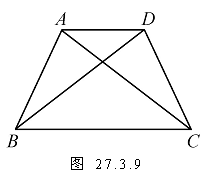
分析　可以通过证明△ABC≌△DCB得出结论．

(请学生写出完整的证明过程)

我们同样可以探索一个梯形具备哪些条件才能成为等腰梯形．

定理　同一条底边上的两个内角相等的梯形是等腰梯形．

已知： 如图27.3.10，在梯形ABCD中，AD∥BC，∠B＝∠C．

求证： 四边形ABCD是等腰梯形．

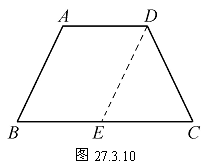
证明　过点D作DE∥AB，交BC于E，则

∠B＝∠DEC(两直线平行，同位角相等)．

因为∠B＝∠C，

所以∠DEC＝∠C，

所以DE＝DC(等角对等边)．

因为AD∥BC，DE∥AB，

所以四边形ABED是平行四边形(平行四边形的定义)，

所以AB＝DE(平行四边形的对边相等)．

因此　AB＝DC，

即四边形ABCD是等腰梯形．

我们还可以得到：

定理两条对角线相等的梯形是等腰梯形．

在第12章中，我们已学过等腰梯形的一些性质．现在也可以用逻辑推理的方法来证明这些性质．

2.尽可能多地说出识别一个四边形为正方形的方法．(说明理由)　

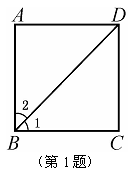
1.如图，在平行四边形ABCD中，∠1＝∠2＝45°．

求证：四边形ABCD是正方形．

5.有一组邻边相等的矩形是正方形．

4.有一个角是直角的菱形是正方形；

3.正方形具有菱形的一切性质：四条边相等，对角线垂直；