
3.弧.
继续观察图2,发现,连结圆上任意两个点可以得到一条弦.同时,这两个点还将圆分成两部分,我们把每一部分叫做圆弧,即:圆上任意两点间的部分叫做圆弧,简称弧.用符号“⌒”表示,如以C、D为端点的弧,记做 .
.
继续引导学生观察会进一步发现,圆的任意一条直径的两个端点分圆成两条弧,每一条弧我们把它叫做半圆;大于半圆的弧叫做优弧,如图中的弧 ,
,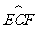 等,小于半圆的弧叫做劣弧.如图中的
等,小于半圆的弧叫做劣弧.如图中的 ,
, 等.
等.
同学们知道怎样画出一个圆么?你都有哪些方法
学生畅所欲言,然后老师动画演示画圆的过程,总结圆定义并板书.
平面上到定点O的距离等于定长的所有点组成的图形叫做圆,定点O叫做圆心,线段OA叫做圆的半径.

以O为圆心的圆,记做⊙O,读作:圆O.
几个概念:
1.弦和直径.
利用上述图形,让学生任意连结圆上两点,就得到一条线段.指出:连结圆上任意两点的线段叫做弦.如线段CD,AB,EF,DF都叫做⊙O的弦.(如图2)

进一步指出:图中弦AB经过圆心O,我们把经过圆心的弦叫做直径.最后让学生观察,得出:直径等于半径的2倍.
观察汽车和皮带转动轮的视频或图片
提问:车轮是什么形状的?
生:圆形(问题简单,一起回答)
教师又问:“为什么车轮要做成圆形呢?难道不可以做成别的形状,比方说三角、四边形等?”
生:“不能!”“它们无法滚动!”
出示小人骑不同轮子小车的课件
师:那我们这样吧,把轮子作成椭圆的,可不可以,同时在黑板上画一椭圆.
生:不行,这样一来,车子前进时,就会一忽儿高,一忽儿低.
教师再进一步启发:为什么做成圆形就不会一下高,一下低呢?
学生思考,同桌讨论,并回答:
因为车轮上的任何一点到轴心的距离都相等的.
18. (2008年江苏省南通市)已知:如图,M是
(2008年江苏省南通市)已知:如图,M是 的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=
的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN= cm.
cm.
(1)求圆心O到弦MN的距离;
16.(2008山东东营)如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有 ( )
A.2个 B.3个 C.4个 D.5 个

17(2008贵州贵阳)24.如图10,已知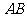 是⊙O的直径,点
是⊙O的直径,点 在⊙O上,且
在⊙O上,且 ,
, .
.
 (1)求
(1)求 的值.
的值.
(2)如果 ,垂足为
,垂足为 ,求
,求 的长.
的长.
(3)求图中阴影部分的面积(精确到0.1).
13..如图所示,AB是半圆O的直径,弦AD、BC相交于点P,∠BPD=α,求 的值.
的值.

中考链接
14(2008湖北襄樊)如图,⊙O中OA⊥BC,∠CDA=25°,则∠AOB的度数为_____.
15(2008 四川 泸州)如图,正方形ABCD是⊙O的内接正方形,点P在劣弧 上不同于点C得到任意一点,则∠BPC的度数是( )
上不同于点C得到任意一点,则∠BPC的度数是( )
A. B.
B.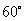 C.
C. D.
D.
12. 如图所示,已知⊙O,线段AB与⊙O交于C、D两点,且OA=OB.求证:AC=BD.
如图所示,已知⊙O,线段AB与⊙O交于C、D两点,且OA=OB.求证:AC=BD.
11.如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.求证:AD·AE=AB·AC

10.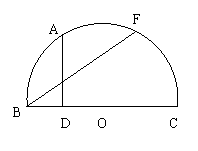 如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是
如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是 的中点,AD⊥BC于点D.求证:AD=
的中点,AD⊥BC于点D.求证:AD= BF.
BF.
9.“圆材埋璧”是我国古代著名数学著作《九章算术》中的一个问题“今有圆材,埋在璧中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何? ”用现在数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长”.请同学们依题意求CD的长.

]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com