
(一)回顾
1、在Rt△ABC中,∠ACB=90°,当∠A确定时,它的对边与斜边之比是______。
锐角A的对边与斜边的比叫做∠A的________,记作_________。即

SinA=___________=________。
2、(1)如图,已知AB是⊙O的直径,点C、D在⊙O上,且
AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
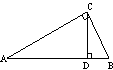
(2)﹙2006成都﹚如图,在Rt△ABC中,∠ACB=90°,
CD⊥AB于点D。已知AC=,BC=2,那么sin∠ACD=( )
 A.
A.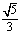 B.
B.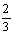 C.
C.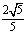 D.
D.
重点:理解余弦、正切的概念
难点:熟练运用锐角三角函数的概念进行有关计算
2、逐步培养学生观察、比较、分析、概括的思维能力.
1、使学生知道当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实.
|
圆的性质 观察与思考 一起探究 大家谈谈 练习 性质1 性质2 性质3 |
这节课你的收获什么?你对弦与弧都有了哪些认识?
2.你认为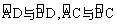 分别具有什么样的关系?和同学说说你的结论和理由.
分别具有什么样的关系?和同学说说你的结论和理由.
学生活动:小组讨论,总结性质
结论:平分弦(不是直径)的直径垂直于弦,并且平分这条弦所对的两条弧
如图,⊙O的直径CD交弦AB(不是直径)与点E,AE=BE.
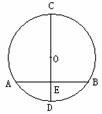
1.你认为CD与AB垂直吗?为什么?
(1)在纸上画出一个圆,并画出任意一条直径及与该直径垂直的一条弦;
(2)将⊙O沿CD所在的直线对折,哪些线段重合?哪些弧重合?由此你得出什么结论?
学生活动:分成小组动手操作,总结得出的结论,并尽力证明
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
让学生做如下操作:
在两张半透明的纸上,分别画出半径相等的⊙O1,⊙O2及相等的两条弦AB,CD,,把两张纸叠放在一起,使⊙O1与⊙O2重合,固定圆心,将一张纸绕圆心旋转适当角度,使弦AB和弦CD重合.
回答: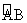 与
与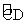 是什么关系?
是什么关系?
思考: (1)在等圆中,如果两条弧相等,那么它们所对的弦相等吗?
(2)在同圆中,相等的弦所对的弧相等吗?等弧所对的弦呢?
由此你能得出什么结论?
学生通过动手发现弦、弧之间的关系:
在同圆或等圆中,相等的弧所对的弦相等;相等的弦所对的优弧和劣弧分别相等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com