
1.课本引入问题,再结合特殊角30°、45°、60°的直角三角形探究直角三角形的边角关系.
(三)教学程序
(二).教材分析:
1.教学重点: 正弦,余弦,正切概念
2.教学难点:用含有几个字母的符号组siaA、cosA、tanA表示正弦,余弦,正切
提高学生对几何图形美的认识.
逐步培养学生观察、比较、分析,概括的思维能力.
初步了解正弦、余弦、正切概念;能较正确地用siaA、cosA、tanA表示直角三角形中两边的比;熟记功30°、45°、60°角的三角函数,并能根据这些值说出对应的锐角度数.
P85 1
(四)巩固再现
1.?在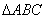 中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(?)
中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(?)
A.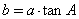 ?B.
?B.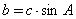 ?C.
?C. ?D.
?D. 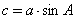
本题主要考查锐解三角函数的定义,同学们只要依据 的图形,不难写出 的图形,不难写出 ,从而可判断C正确. ,从而可判断C正确. |
2. 在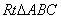 中,∠C=90°,如果
中,∠C=90°,如果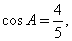 那么
那么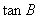 的值为(?)
的值为(?)
 A.
A.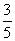 ?B.
?B.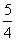 ?C.
?C.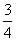 ?D.
?D.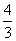
|
分析? 本题主要考查锐解三角函数及三角变换知识。 其思路是:依据条件 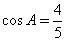 ,可求出 ,可求出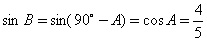 ;再由 ;再由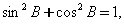 ,可求出 ,可求出 ,从而 ,从而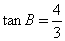 ,故应选D. ,故应选D. |
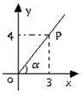
3、如图:P是∠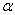 的边OA上一点,且P
的边OA上一点,且P
点的坐标为(3,4),则cos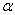 =_____________.
=_____________.
4、P81 练习1、2、3
(三)教学互动
例2: 如图,在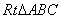 中,
中, 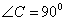 ,BC=6,
,BC=6, 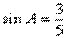 。求CosA和tanB的值.
。求CosA和tanB的值.
解:
.
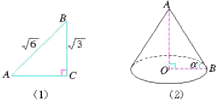
例3:(1)如图(1), 在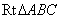 中,
中,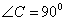 ,
,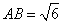 ,
,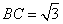 ,求
,求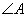 的度数.
的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的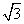 倍,求
倍,求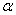 .
.
(二)探索新知
一般地,当∠A取其他一定度数的锐角时,它的邻边与斜边的比是否也是一个固定值?
如图:Rt△ABC与Rt△A`B`C`,∠C=∠C` =90o,∠B=∠B`=α,

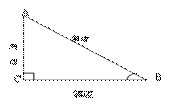 那么
那么 与
与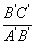 有什么关系?
有什么关系?
分析:由于∠C=∠C` =90o,∠B=∠B`=α,
所以Rt△ABC∽Rt△A`B`C`,
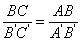 ,即
,即 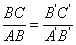
结论:在直角三角形中,当锐角B的度数一定时,不管三角形的大小如何,∠B的邻边与斜边的比也是一个固定值。
如图,在Rt△ABC中,∠C=90o,把锐角B的邻边与斜边的比叫做∠B的余弦,记作cosB即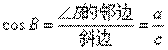
类似的, 当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比也是一个_________。
把∠A的对边与邻边的比叫做∠A的正切.记作tanA,即
tanA=_______________=_____
锐角A的正弦,余弦,正切都叫做∠A的锐角三角函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com