(二)实践探索

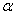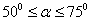要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足， (如图).现有一个长6m的梯子，问:

(1)使用这个梯子最高可以安全攀上多高的墙(精确到0. 1 m)　

(2)当梯子底端距离墙面2.4 m时，梯子与地面所成的角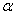等于多少(精确到1^o)　这时人是否能够安全使用这个梯子　

　 引导学生先把实际问题转化成数学模型

然后分析提出的问题是数学模型中的什么量

在这个数学模型中可用学到的什么知识来求

未知量？

　　 几分钟后，让一个完成较好的同学示范。

(一)复习引入

1．直角三角形中除直角外五个元素之间具有什么关系？请学生口答．

2、在中Rt△ABC中已知a=12　 ,c=13 求角B应该用哪个关系？请计算出来。

重点：要求学生善于将某些实际问题中的数量关系，归结为直角三角形元素之间的关系，从而利用所学知识把实际问题解决．

难点：实际问题转化成数学模型

3、渗透数学来源于实践又反过来作用于实践的观点，培养学生用数学的意识

2、逐步培养学生分析问题、解决问题的能力．

1、使学生会把实际问题转化为解直角三角形问题，从而会把实际问题转化为数学问题来解决．

课题　 28.2 解直角三角形(二)

(四)总结与扩展

1．请学生小结：在直角三角形中，除直角外还有五个元素，知道两个元素(至少有一个是边)，就可以求出另三个元素．

2．出示图表，请学生完成

	a	b	c	A	B
1	√	√
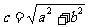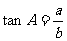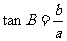2	√		√
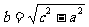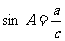3	√	b=a•cotA		√
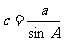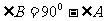4	√	b=a•tanB			√
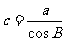5		√	√
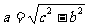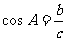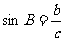6	a=b•tanA	√		√
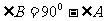7	a=b•cotB	√			√
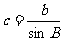8	a=c•sinA	b=c•cosA	√	√
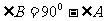9	a=c•cosB	b=c•sinB	√		√
10	不可求	不可求	不可求	√	√

注：上表中“√”表示已知。

(二)教学过程

　1．我们已掌握Rt△ABC的边角关系、三边关系、角角关系，利用这些关系，在知道其中的两个元素(至少有一个是边)后，就可求出其余的元素．这样的导语既可以使学生大概了解解直角三角形的概念，同时又陷入思考，为什么两个已知元素中必有一条边呢？激发了学生的学习热情．

2．教师在学生思考后，继续引导“为什么两个已知元素中至少有一条边？”让全体学生的思维目标一致，在作出准确回答后，教师请学生概括什么是解直角三角形？(由直角三角形中除直角外的两个已知元素，求出所有未知元素的过程，叫做解直角三角形)．

3．例题

例　 1在△ABC中，∠C为直角，∠A、∠B、∠C所对的边分别为a、b、c，且b=，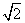

a=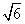，解这个三角形．

解直角三角形的方法很多，灵活多样，学生完全可以自己解决，但例题具有示范作用．因此，此题在处理时，首先，应让学生独立完成，培养其分析问题、解决问题能力，同时渗透数形结合的思想．其次，教师组织学生比较各种方法中哪些较好，选一种板演．

解　 ∵tanA===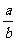

∴　

∴　

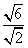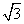
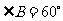
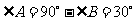
∴C=2b=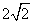

例　 2在Rt△ABC中， ∠B =35，b=20，解这个三角形．

　引导学生思考分析完成后，让学生独立完成

　在学生独立完成之后，选出最好方法，教师板书．

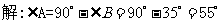
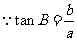
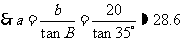
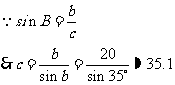
完成之后引导学生小结“已知一边一角，如何解直角三角形？”

答：先求另外一角，然后选取恰当的函数关系式求另两边．计算时，利用所求的量如不比原始数据简便的话，最好用题中原始数据计算，这样误差小些，也比较可靠，防止第一步错导致一错到底

注意：例1中的b和例2中的c都可以利用勾股定理或其它三角函数来计算，但计算出的值可能有些少差异，这都是正常的。　

4．巩固练习

　P91

说明：解直角三角形计算上比较繁锁，条件好的学校允许用计算器．但无论是否使用计算器，都必须写出解直角三角形的整个过程．要求学生认真对待这些题目，不要马马虎虎，努力防止出错，培养其良好的学习习惯．

(一)复习引入

1．在三角形中共有几个元素？

2．直角三角形ABC中，∠C=90°，a、b、c、∠A、∠B这五个元素间有哪些等量关系呢？

(1)边角之间关系

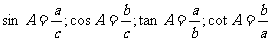
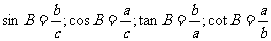
如果用表示直角三角形的一个锐角，那上述式子就可以写成.

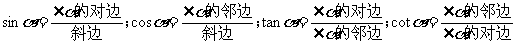
(2)三边之间关系

　a² +b² =c² (勾股定理)

　(3)锐角之间关系∠A+∠B=90°．

　以上三点正是解直角三角形的依据，通过复习，使学生便于应用．