7、下列等式中正确的是(　 )

(A)　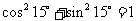　　　 (B)cos30°+cos45°=cos75°

(C)　　　 (D)2cot22°30＇=cot45°=1

根，则此三角形为　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．等腰三角形　　　　　　　　　　　 B．直角三角形

C．等腰直角三角形　　　　　　　　　 D．等边三角形

6、在Rt△ABC中，∠C=90°，已知a和A，则下列关系式中正确的是(　)

A. c＝α·sinA　　 B. c＝　 C. c＝α·cosB　　 D. c＝

5、下列各式正确的是　　　　　　　　　　　　　　　　　　　 (　)

A．sin46°＜cos46°＜tg46°　　　 B．sin46°＜tg46°＜cos46°

C．tg46°＜cos46°＜sin46°　　　 D．cos46°＜sin46°＜tg46°

4、在Rt△ABC中，∠C＝90°，a、b、c分别为∠A、∠B、∠C的对边，

　 则下列各式正确的是　　　　　　　　　　　　　　　　　　　　 (　)

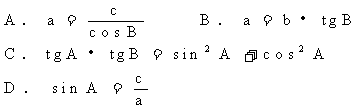
3、已知△ABC中，∠C=90°，tanA·tan 50°＝1，那么∠A的度数是(　　)

A. 50°　　　 B. 40°　　　 C. ()°　　　 D. ()°

1、在Rt△ABC中，∠C=90°，a＝1，c＝4,则sinA的值是(　　)

A. 　　　 B.　　　　C.　 　　　 D.

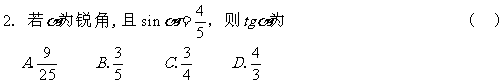
P97　 8

(三)巩固再现

1、P95　 2

2、利用土埂修筑一条渠道，在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分)，已知渠道内坡度为1∶1.5，渠道底面宽BC为0.5米，求：

　①横断面(等腰梯形)ABCD的面积；

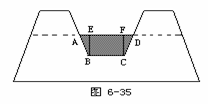　②修一条长为100米的渠道要挖去的土方数．

(一)复习引入

1．讲评作业：将作业中学生普遍出现问题之处作一讲评．

2．创设情境，导入新课．

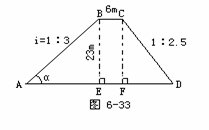
例　 同学们，如果你是修建三峡大坝的工程师，现在有这样一个问题请你解决：如图6-33

　水库大坝的横断面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i=1∶2.5，求斜坡AB的坡面角α，坝底宽AD和斜坡AB的长(精确到0.1m)．

　　 同学们因为你称他们为工程师而骄傲，满腔热情，但一见问题又手足失措，因为连题中的术语坡度、坡角等他们都不清楚．这时，教师应根据学生想学的心情，及时点拨．

(二)教学互动

通过前面例题的教学，学生已基本了解解实际应用题的方法，会将实际问题抽象为几何问题加以解决．但此题中提到的坡度与坡角的概念对学生来说比较生疏，同时这两个概念在实际生产、生活中又有十分重要的应用，因此本节课关键是使学生理解坡度与坡角的意义．

1． 坡度与坡角

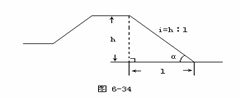
结合图6-34，教师讲述坡度概念，并板书：坡面的铅直高度h和水平宽度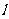的比叫做坡度(或叫做坡比)，一般用i表示。即i＝，常写成i=1：m的形式如i=1:2.5

把坡面与水平面的夹角α叫做坡角．

　引导学生结合图形思考，坡度i与坡角α之间具有什么关系？

　答：i＝＝tan

　这一关系在实际问题中经常用到，教师不妨设置练习，加以巩固．

练习(1)一段坡面的坡角为60°，则坡度i=______；

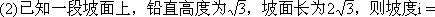　 ______，坡角______度．

　为了加深对坡度与坡角的理解，培养学生空间想象力，教师还可以提问：

　(1)坡面铅直高度一定，其坡角、坡度和坡面水平宽度有什么关系？举例说明．

　(2)坡面水平宽度一定，铅直高度与坡度有何关系，举例说明．

　答：(1)

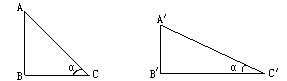　如图，铅直高度AB一定，水平宽度BC增加，α将变小，坡度减小，

因为 tan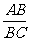＝，AB不变，tan随BC增大而减小

(2)与(1)相反，水平宽度BC不变，α将随铅直高度增大而增大，tanα

　 也随之增大，因为tan=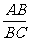不变时，tan随AB的增大而增大

2．讲授新课

　 引导学生回头分析引题，图中ABCD是梯形，若BE⊥AD，CF⊥AD，梯形就被分割成Rt△ABE，矩形BEFC和Rt△CFD，AD=AE+EF+FD，AE、DF可在△ABE和△CDF中通过坡度求出，EF=BC=6m，从而求出AD．

　　 以上分析最好在学生充分思考后由学生完成，以培养学生逻辑思维能力及良好的学习习惯．

　　 坡度问题计算过程很繁琐，因此教师一定要做好示范，并严格要求学生，选择最简练、准确的方法计算，以培养学生运算能力．

　解：作BE⊥AD，CF⊥AD，在Rt△ABE和Rt△CDF中，

∴AE=3BE=3×23=69(m)．

　FD=2.5CF=2.5×23=57.5(m)．

　∴AD=AE+EF+FD=69+6+57.5=132.5(m)．

　 因为斜坡AB的坡度i＝tan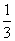＝≈0.3333，　

α≈18°26′

　答：斜坡AB的坡角α约为18°26′，坝底宽AD为132.5米，斜坡AB的长约为72.7米．

其实这是旧人教版的一个例题，由于新版里这样的内容和题目并不少，但是对于题目里用的术语新版少提，基于学生的接受情况应插讲这一内容。

重点：解决有关坡度的实际问题．

难点：理解坡度的有关术语．