
4.总结提高
[本节课重点是让学生掌握如何把实际问题转化为数学问题,数学建模思想必不可少,具体操作方法就是抽象出几何图形,就本课而言是主要是两个三角形的两种不同组合图形。此外在解直角三角形是,也顺带渗透了方程思想。]
(1)数学建模及方程思想
从实际问题抽象出数学模型,将实际问题转化为数学问题求解;
解直角三角形常结合用方程。
(2)解题方法小结
A.把实际问题转化为数学问题的两个方面;(图形转化,条件转化)
B.把数学问题转化为解直角三角形的处理方法.(构造直角三角形)
(将实际问题转化为数学问题,关键要画好示意图,从实际问题抽象出数学模型,如果是单个直角三角形,则直接解直角三角形,如果是一般三角形,甚至是梯形或组合图形,则通过作高将其转化为直角形再求解,而解直角三角形的常用方法是结合方程进行计算)
3. 拓展延伸
拓展延伸
[加入这道中考题,除了巩固所学,更重要的是让学生对中考题有一个正确认识,中考题不等于难题。]
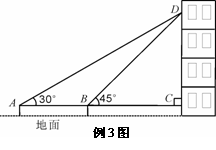
[例3](2008芜湖)在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后, 又在点B处测得条幅顶端D的仰角为45°,已知点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据: )
)
(本题是在上述问题基础上稍加变化,要注意的是所求问题为条幅顶端D到地面的距离,而非条幅DC的长度,所以解题时将问题放在Rt△ACD与Rt△BCD中求解,求得CD后不要忘记加上A、B、C离地面的高度1.44米)
2.例题分析
 [设计说明:联系实际,对问题情境的理解需要学生具有一定的空间想象能力,在审题过程中自然引出仰角、俯角概念,逐步向学生渗透数学建模思想,帮助学生从实际问题中,抽象出数学模型,将实际问题转化为数学问题来解决。例1讲解,先引导学生分析,然后借助多媒体逐步展示解题过程,规范书写格式,强调解题完整性。变题1与例1是交换题目条件与结论,情境不变,分别求桥长与飞机高。变题2-3情境有所变化,由测桥变为测楼,所求问题是飞机高及飞机到楼房距离。以上问题的解题关键在于转化实际问题为数学问题,着重是示意图的画法及让学生说出题中每句话对应图中的哪条边或哪个角(包括已知什么和求什么),进而利用解直角三角形知识解决问题,并在解题后及时加以归纳,挖掘图形结构及条件的特点。]
[设计说明:联系实际,对问题情境的理解需要学生具有一定的空间想象能力,在审题过程中自然引出仰角、俯角概念,逐步向学生渗透数学建模思想,帮助学生从实际问题中,抽象出数学模型,将实际问题转化为数学问题来解决。例1讲解,先引导学生分析,然后借助多媒体逐步展示解题过程,规范书写格式,强调解题完整性。变题1与例1是交换题目条件与结论,情境不变,分别求桥长与飞机高。变题2-3情境有所变化,由测桥变为测楼,所求问题是飞机高及飞机到楼房距离。以上问题的解题关键在于转化实际问题为数学问题,着重是示意图的画法及让学生说出题中每句话对应图中的哪条边或哪个角(包括已知什么和求什么),进而利用解直角三角形知识解决问题,并在解题后及时加以归纳,挖掘图形结构及条件的特点。]
[例1]直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB.
[分析]如图所示,要求AB长,先设法求出边AO与BO的长,然后相减即可,由条件可得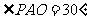 ,
, ,又因为PO=450米,可选择上述两特殊角正切分别求得AO与BO.
,又因为PO=450米,可选择上述两特殊角正切分别求得AO与BO.
[解]由题意得,
 ,
,
 ,
, ,
, ,
,
 答:大桥的长AB为
答:大桥的长AB为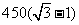 米.
米.
(就题目中出现的“俯角”先通过链接加以介绍,引导学生分析,强调解题完整,要写“答”,注意单位,指明这些都是中考失分的重要因素)
 变题1:直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45
°,求飞机的高度PO.
变题1:直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45
°,求飞机的高度PO.
请学生自行分析解决,并交流不同解法,引导学生注意方程思想的运用.
 (本题应注意方程思想的运用,可设所求PO长为x,由45度角的正切或直接由“等角对等边”可求得OB也等于x,然后再由30度角的正切列出方程,即
(本题应注意方程思想的运用,可设所求PO长为x,由45度角的正切或直接由“等角对等边”可求得OB也等于x,然后再由30度角的正切列出方程,即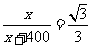 ,熟练后也可以直接列
,熟练后也可以直接列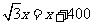 ,所以
,所以 )
)
变题2:直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和60°,求飞机的高度PO.
引导学生将问题转化为两个直角三角形组合图形中加以解决,可割可补.
(本题估计学生会出现两种不同解法,割或补,即过A作AC⊥PO,要求PO长,此时CO=AB=200,只需求出PC即可;或是过P作PC垂直BA延长线于点C,求出AC。不管哪种方法,必须注意所设未知数是哪条边,如果不是直接设PO为未知数,则一定要注意最后的结果必须是PO的长,结果为 )
)
[注重变题2、3的一题多解教学,从学生作业中展示不同解法,让学生有更为广阔的解题思路。]
 变题3:直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离.
变题3:直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离.
找出等量关系,列方程.
(列方程关键在于找出等量关系,本题可以以AB长为等量关系,充分利用好45度角的特点,即PD=AD,如果设PD=x,则AD=x,由30度角可表示 ,从而可以列出方程
,从而可以列出方程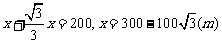 ;设BD=x,则AD=PD=200-x,
;设BD=x,则AD=PD=200-x,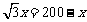 ,得
,得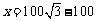 ,不能忘记求PD)
,不能忘记求PD)
根据以上解题过程,列举四题中三个示意图,分析归纳这类问题的共同点.从而初步渗透数学建模及方程思想,并归纳出这类图形的结构特点.
(将例1及3个相关变题中的图形列举后加以分析,从每个问题所提供的条件特点,结合图形结构特征,可归纳出这类问题:(1)示意图为有一个公共边的两个直角三角形,分布位置有两种,位于公共边同侧或异侧;(2)所给条件一般为两角一边,且边一般为已知角的邻边或对边(非直角三角形斜边),此时选用的三角函数关系多为正切)
[例2]学生小王帮在测绘局工作的爸爸买了一些仪器后与同学在环西文化广场休息,看到濠河对岸的电视塔,他想用手中的测角仪和卷尺不过河测出电视塔空中塔楼的高度.现已测出∠ADB=40°,由于不能过河,因此无法知道BD的长度,于是他向前走50米到达C处测得∠ACB=55°,但他们在计算中碰到了困难,请大家一起想想办法,求出电视塔塔楼AB的高.(参考数据: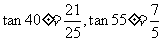 )
)


[这是一道原创题,目的一是让学生明白实际问题中的角不一定是特殊角,二是结合本地的标示性建筑,简单介绍南通电视塔信息:1985年开始兴建,89年建成,为当时中国第三座,江苏省第一座钢筋混凝土结构的电视塔,以此激发学生自豪感,更加热爱家乡,努力学习。]
(电视塔中上部建有可供游人参观游览的空中塔楼,我们的问题就在这个塔楼的高度上)
(本题中所提供的条件仍属于两角一边问题,符合我们所归纳的特点,但所提供角度不是特殊角,计算时要加以注意。同样本题也是解法不唯一,学生完成后交流时,可展示不同解法。如果设AB=x,则得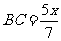 ,再由
,再由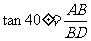 可得方程
可得方程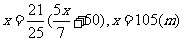 ;如果设BC=x,则可以以AB作为等量关系,列出方程
;如果设BC=x,则可以以AB作为等量关系,列出方程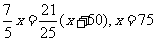 ,再求得
,再求得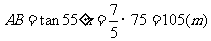 ,比较两种方法,方法一更直接,方法二计算更方便)
,比较两种方法,方法一更直接,方法二计算更方便)
1.导入新课
[设计说明:明确本节课学习目标,复习解直角三角形的概念及相关方法原则,为接下来的学习做好充分准。]
展示学习目标,交流课前预习内容:解直角三角形中常用的数量关系及相关原则方法.
(课前布置预习作业,角、边共同回答,其它直接交流,强调三角函数关系形式灵活,可写为比的形式,也可写为乘积形式)
(解直角三角形原则(1)、(2)学生齐声回答)
(交流自己添加条件解直角三角形问题挑选所给条件不同形式的作业展示,主要是“一边一角”,“两边”等类型,归纳强调已知条件至少有一个必须是边)
2.难点:能够准确分析问题并将实际问题转化为数学模型.
1.重点:应用解直角三角形的有关知识解决观测问题.
知识目标:了解仰角、俯角概念,能应用解直角三角形解决观测中的实际问题.帮助学生学会把实际问题转化为解直角三角形问题,从而把实际问题转化为数学问题来解决.
能力目标:逐步培养学生分析问题、解决问题的能力.渗透数学建模及方程思想和方法,能将实际问题中的数量关系转化为直角三角形中元素之间的关系.
情感与价值观:渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识,同时激发学生对自己家乡的热爱之情及自豪感,更好的激励学习.
4. 如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 .
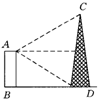
3.如图3,从地面上的C,D两点测得树顶的仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).
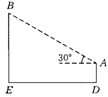
2.如图2,在离铁塔BE120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE=_________(根号保留).


|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com